Heap 구조체
- 우선순위 큐를 위해 만들어진 자료구조
- 여러 값들 중 최솟값이나 최댓값을 빠르게 탐색하기 위한 자료구조
- 반정렬 상태를 유지
- 이진 트리와는 달리, 중복된 값을 허용
- 이진 트리에서 특정한 조건을 갖춘 구조체
- 트리의 높이 h가 h-1 까지 완전 이진 트리
- 모든 leaf 노드의 깊이는 h 이거나 h-1
- 깊이 h의 모든 leaf 노드들의 경로는 h-1의 모든 leaf 노드보다 왼편에 있다
Heap 종류
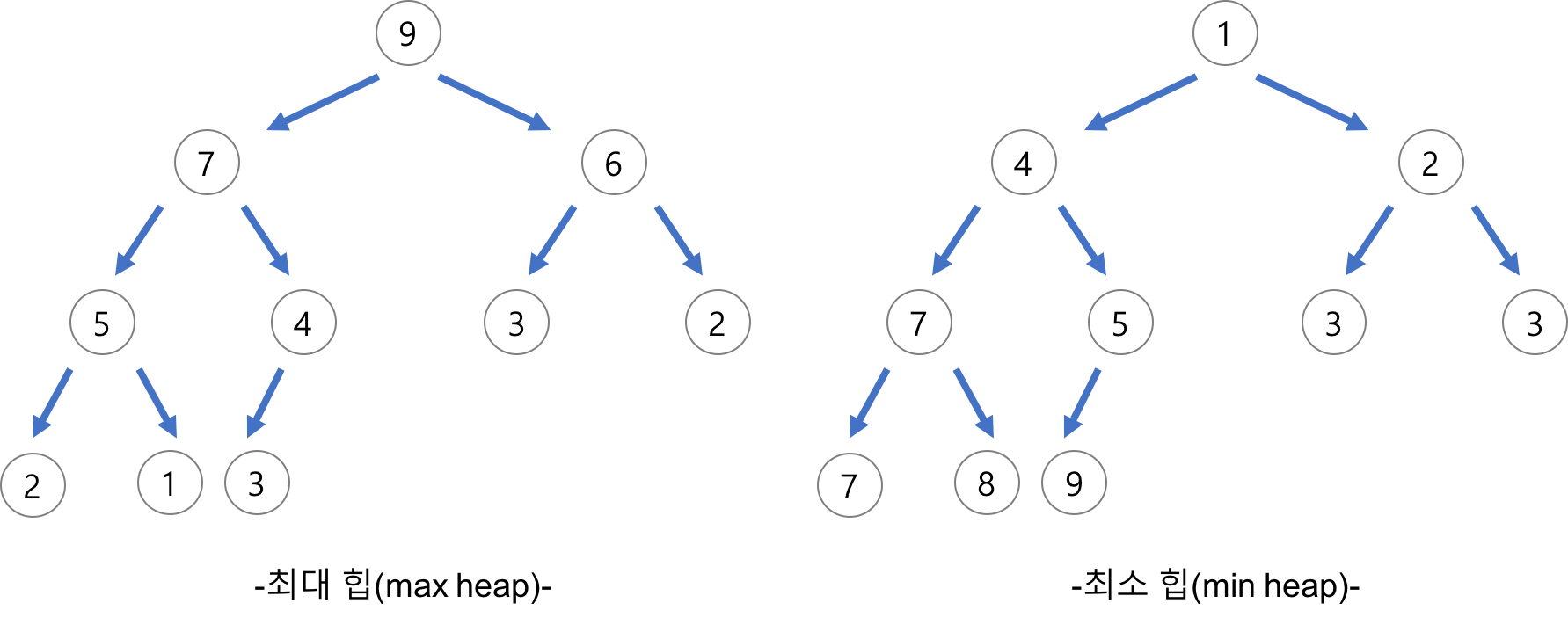
- 최대 힙
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 완전 이진트리
- 부모노드 키 >= 자식노드 키
- 최소 힙
- 자식 노드의 키 값이 부모 노드의 키 값보다 크거나 같은 완전 이진트리
- 자식노드 키 >= 부모노드 키
Heap 구현
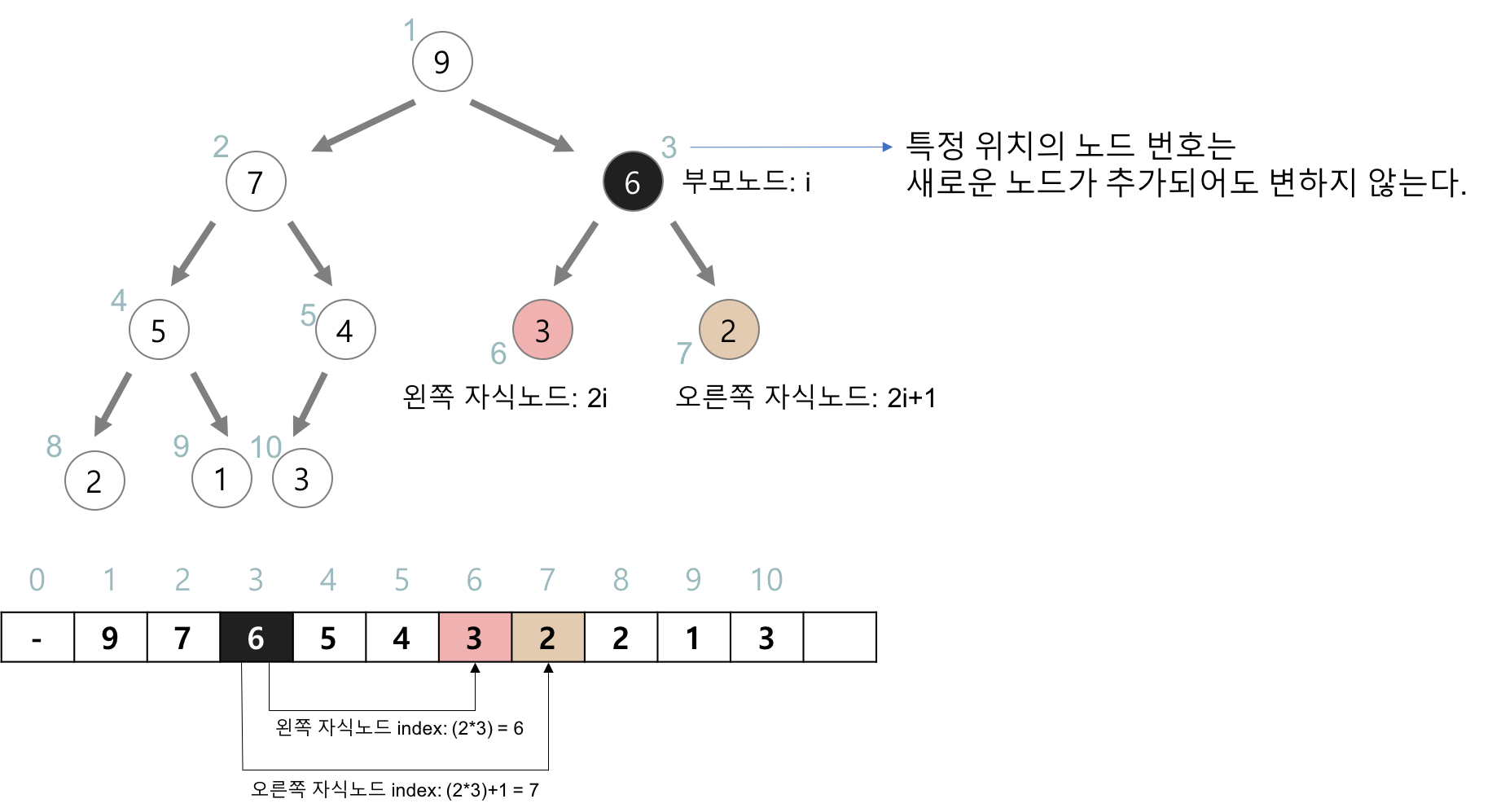
- 기본적으로 자료구조는 배열(Array)
- 첫 번째 인덱스(index 0)는 사용하지 않음
- 아래 표는 부모 노드와 자식 노드의 관계
| 인덱스 |
계산 |
| 왼쪽 자식의 인덱스 |
= 부모 인덱스 * 2 |
| 오른쪽 자식의 인덱스 |
= 부모 인덱스 * 2 + 1 |
| 부모의 인덱스 |
= 자식 인덱스 / 2 |
// 힙 안에 저장된 요소의 개수
#define MAX_ELEMENT 200
// 원소
typedef struct{
int key;
} element;
// 타입 선언
typedef struct{
element heap[MAX_ELEMENT];
int heap_size;
} HeapType;
// 힙의 생성
HeapType heap1;
Heap 삽입
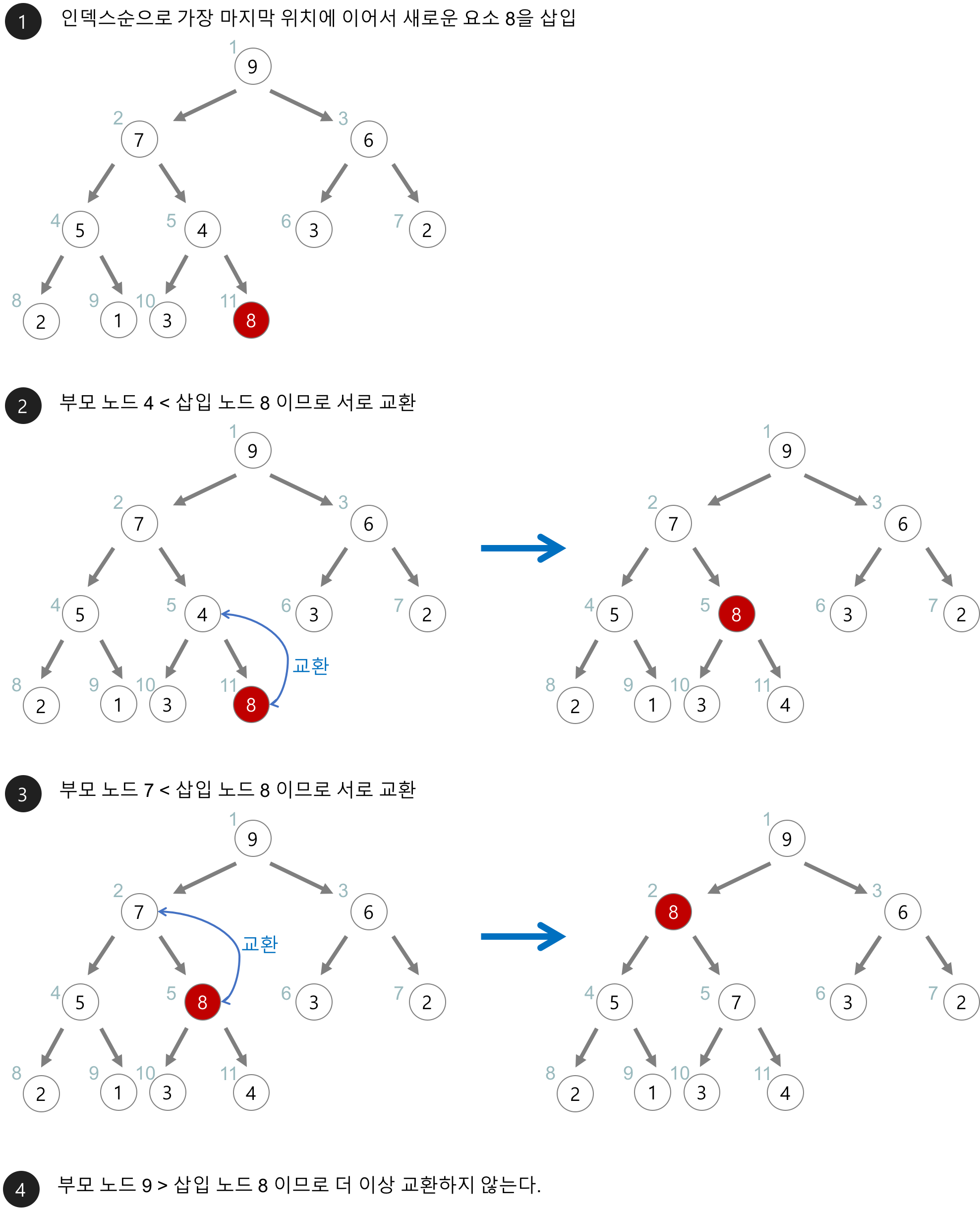
- 힙에 새로운 요소가 들어오면, 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다.
- 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
/* 현재 요소의 개수가 heap_size인 힙 h에 item을 삽입한다. */
// 최대 힙(max heap) 삽입 함수
void insert_max_heap(HeapType *h, element item){
int i; // i번째 인덱스에 새 노드 삽입
i = ++(h->heap_size); // 힙 크기를 하나 증가
/* 트리를 거슬러 올라가면서 부모 노드와 비교하는 과정 */
// i가 루트 노트(index: 1)이 아니고, 삽입할 item의 값이 i의 부모 노드(index: i/2)보다 크면
while((i != 1) && (item.key > h->heap[i/2].key)){
// i번째 노드와 부모 노드를 교환환다.
h->heap[i] = h->heap[i/2];
// 한 레벨 위로 올라단다.
i /= 2;
}
h->heap[i] = item; // 새로운 노드를 삽입
}
Heap 삭제
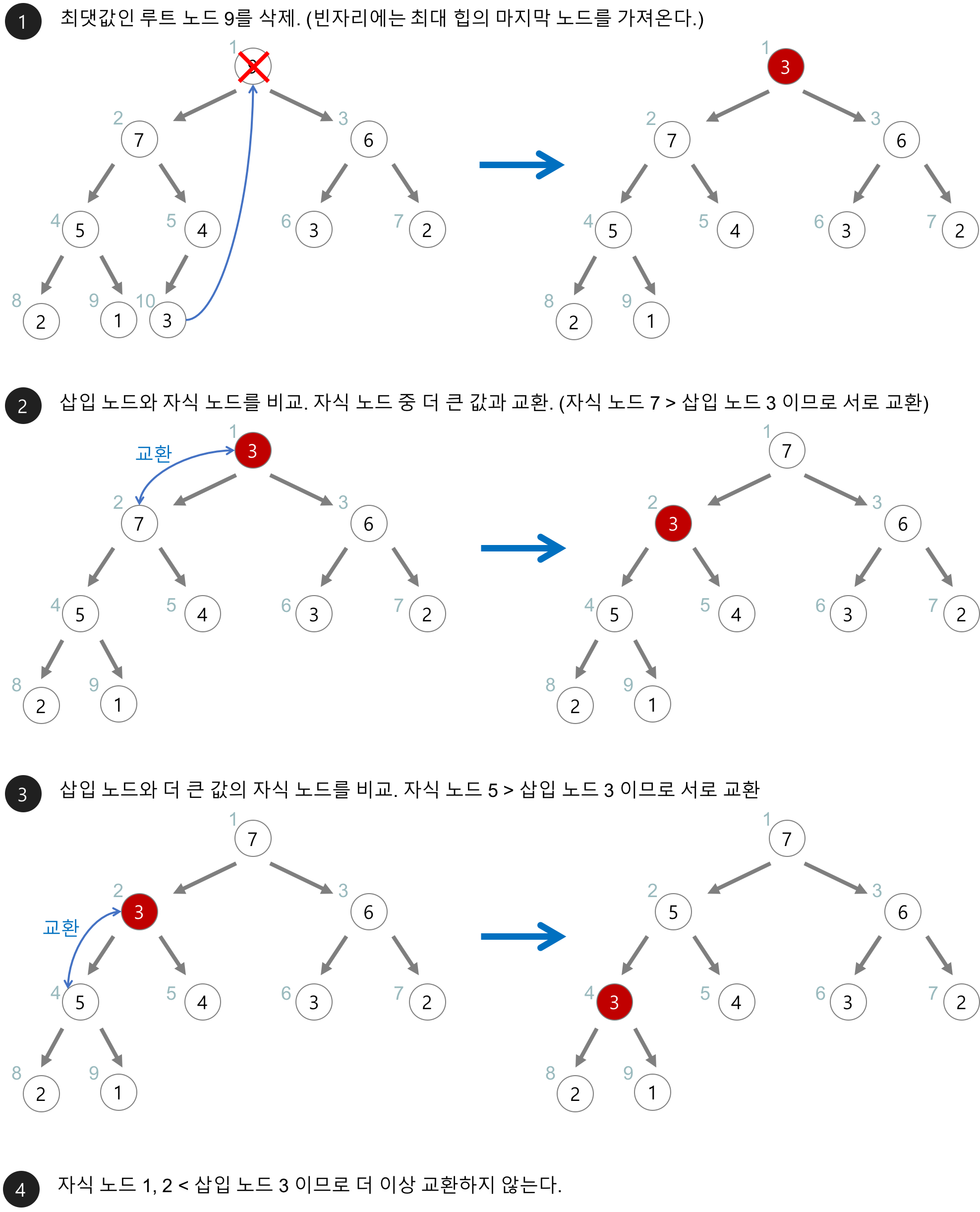
- 최대 힙에서 삭제는 최댓값, 즉 루트 노드의 삭제
- 삭제된 루트 노드에 배열 상 마지막 노드를 가져온다
- 힙을 교환하며 재구성 한다
// 최대 힙(max heap) 삭제 함수
element delete_max_heap(HeapType *h){
int parent, child;
element item, temp;
item = h->heap[1]; // 루트 노드 값을 반환하기 위해 item에 할당
temp = h->heap[(h->heap_size)--]; // 마지막 노드를 temp에 할당하고 힙 크기를 하나 감소
parent = 1; // 첫번째 부모
child = 2; // 첫번째 자식
while(child <= h->heap_size){
// 현재 노드의 자식 노드 중 더 큰 자식 노드를 찾는다. (루트 노드의 왼쪽 자식 노드(index: 2)부터 비교 시작)
if( (child < h->heap_size) && ((h->heap[child].key) < h->heap[child+1].key) ){
// 오른쪽 child가 더 크면 옆으로 이동
child++;
}
// 더 큰 자식 노드보다 마지막 노드가 크면, while문 중지
if( temp.key >= h->heap[child].key ){
break;
}
// 더 큰 자식 노드보다 마지막 노드가 작으면, 부모 노드와 더 큰 자식 노드를 교환
h->heap[parent] = h->heap[child];
// 한 단계 아래로 이동
parent = child;
// 업데이트 된 부모의 왼쪽 인덱스
child *= 2;
}
// 마지막 노드를 재구성한 위치(넣기로 한 위치)에 삽입
h->heap[parent] = temp;
// 최댓값(루트 노드 값)을 반환
return item;
}
Priority Queue 우선순위 큐
- 일반적인 큐는 First In First Out
- 우선순위 큐는 삽입된 순서와 무관하게 우선순위가 높은 데이터나 먼저 Out
- Heap 자료 구조를 통해 구현 가능
- Priority Queue는 배열 안의 원소을 모두 정렬하는 것이 아니라, 최대/최소값이 head에 오도록하는 컨테이너다
왜 Priority Queue는 Array나 LinkedList로 구현하지 않는가?
- 배열로 구현
- 우선 순위가 가장 높은 맨 앞의 인덱스를 Out까지는 가능
- 그러나 삽입하는 과정 적절한 삽입 위치를 찾고, 또 삽입하기 위해 인덱스를 모두 한 칸씩 미뤄야 함
- 링크리스트로 구현
- 역시 최우선 순위의 반환은 쉬움
- 그러나 배열과 마찬가지로 삽입 위치를 찾는데 낭비
- 삭제는 O(1)
- 삽입은 O(n)
출처



