Juyong Jeong

Juyong Jeong

💻Game Client Programmer

STL - Map, Set

  • 이미 정렬되어 있는 데이터를 대상으로 탐색
  • 중간 값인 pivot을 기준으로 left와 right으로 나누어 탐색
    • 값을 찾을 때까지 위의 과정을 반복

AVL Tree

  • 왼쪽 서브 트리와 오른쪽 서브 트리의 균형 인수가 -1 <= h <= 1 인 트리
    • 균형 인수(BF/Balance Factor): 왼쪽 서브 트리의 높이에서 오른쪽 서브 트리의 높이를 뺀 값
    • 높이 균형 성질(height-balance property) : 트리 T의 모든 내부 노드(internal node) v에 대하여 v의 자식 노드들의 높이 차이가 최대 1
  • Self Balancing
    • 균형이 깨지는 경우를 LL LR RR RL로 나누어 회전을 통해 다시 균형을 맞춤
  • 자료 개수가 증가하면 트리의 높이가 높아지는 문제점

2-3 Tree

post_thumbnail

  • 하나의 노드가 1개 혹은 2개의 키를 가진다
  • 하나의 노드는 2개 혹은 3개의 child를 가진다
  • 키는 작은 것에서 큰 것으로 정렬한다
  • 모든 leaf들은 가장 낮은, 그리고 동일한 레벨에 있다
  • 소거 혹은 삽입이 발생하면 밸런싱한다
    • bottom-up 방식으로 밸런싱
    • 아래 예시 참조

삽입 예시 1

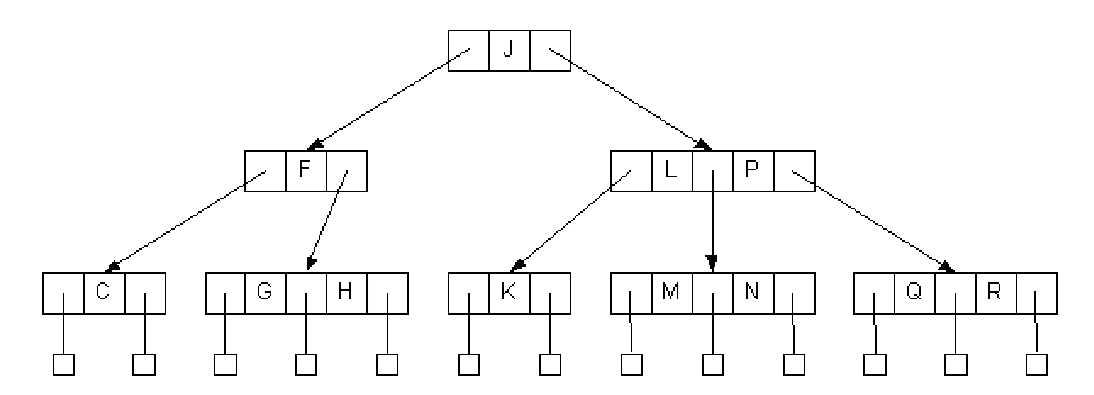
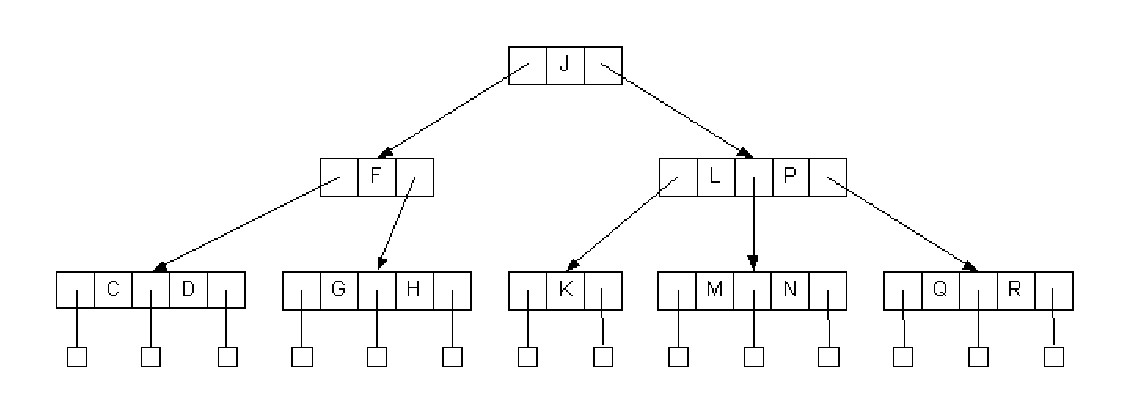
post_thumbnail post_thumbnail

  • 새로운 원소 D를 삽입

삽입 예시 2

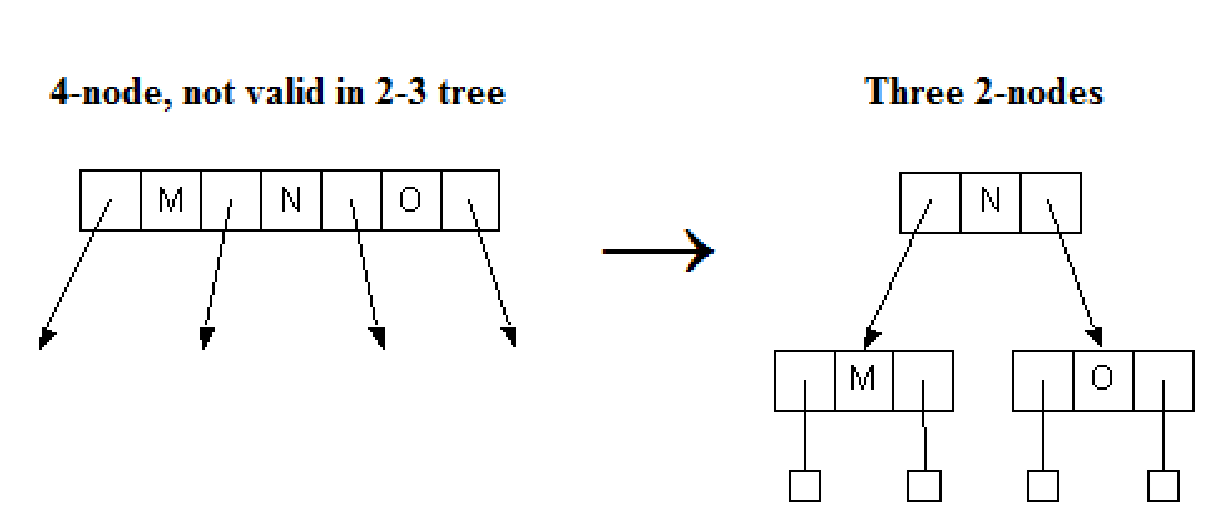
post_thumbnail

  • 새로운 원소 O을 삽입
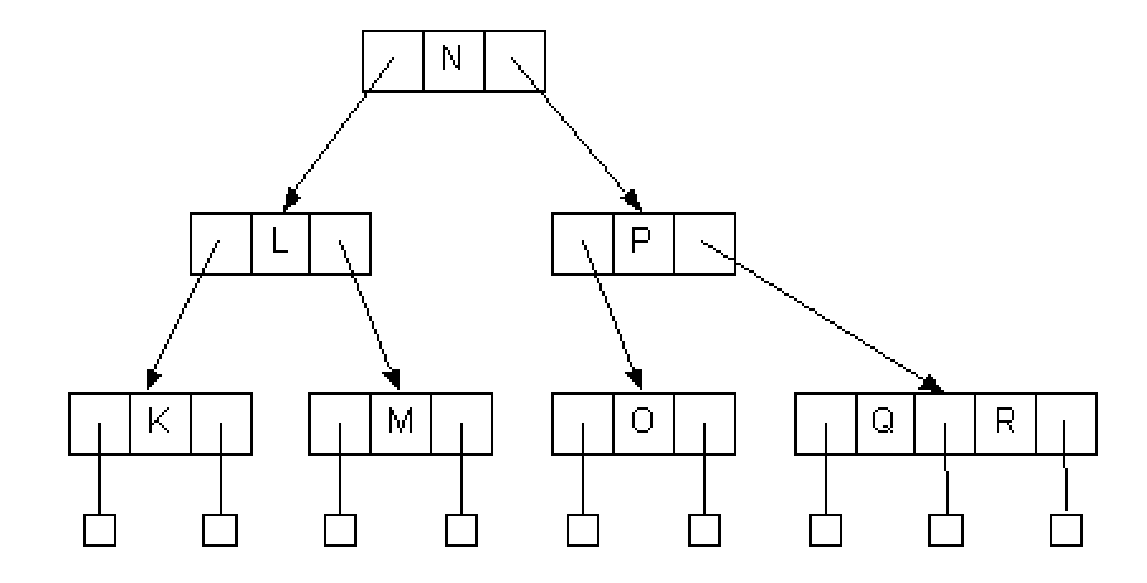
  • 4-node를 분리하고 N이 위로 올라감 post_thumbnail
  • 한 레벨 위로 올라간 N은 L.P와 동일 계층이 됨
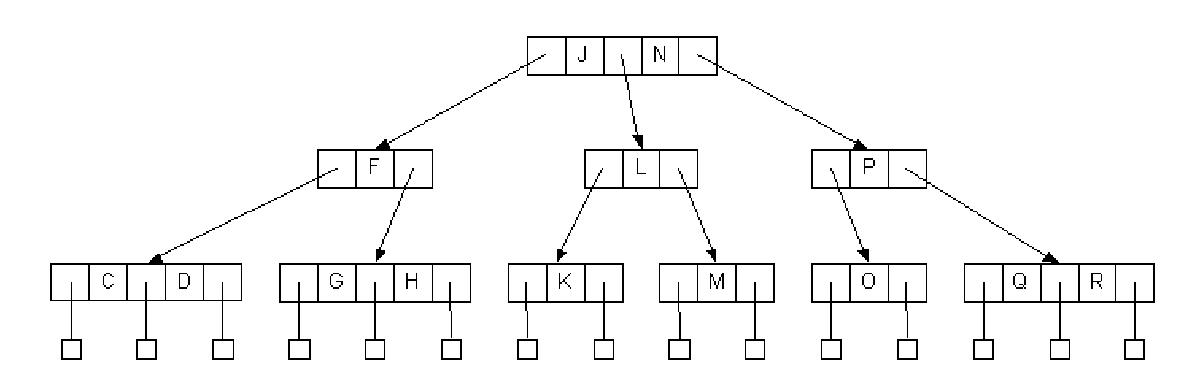
  • N은 다시 한 레벨 더 위로 올라감 post_thumbnail
  • N이 J와 같은 레벨로 상승하면서 종료

2-3-4 Tree

  • 2-3 Tree와 유사
  • 하나의 노드가 1~3개의 키를 가진다
  • 하나의 노드가 2~4개의 Child를 가진다
  • 모든 leaf들은 가장 낮은, 그리고 동일한 레벨에 있다
  • top-down 방식으로 밸런싱

삽입 예시

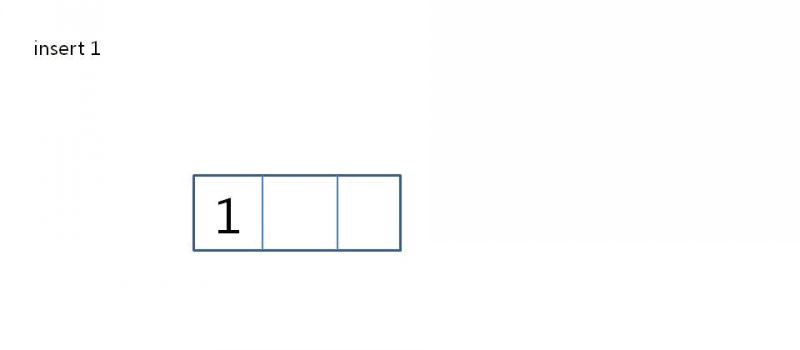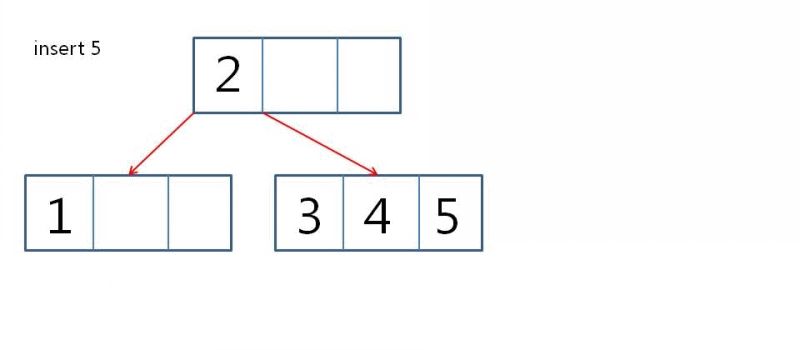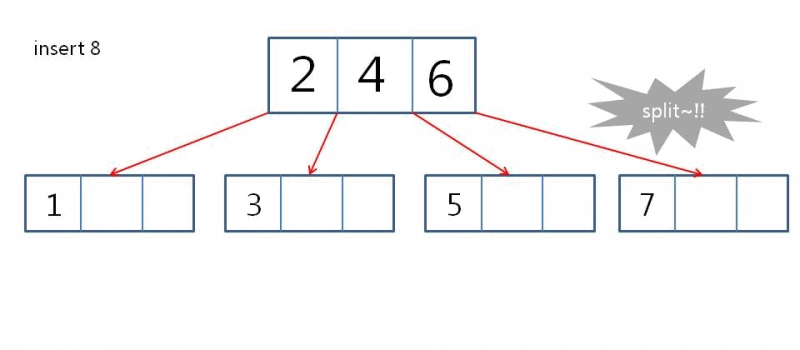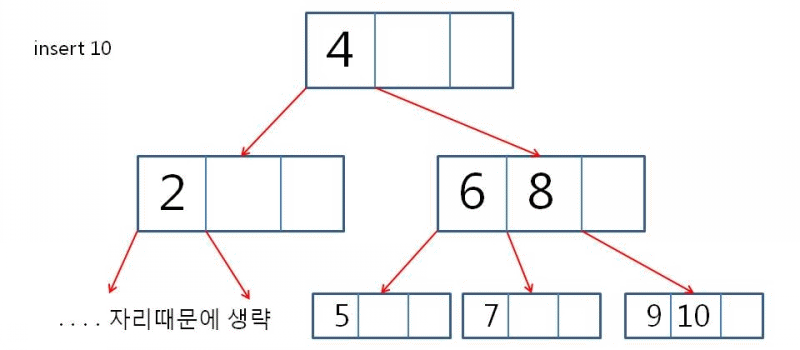
post_thumbnail

  • 4-node가 2-node with 2 children으로 변환한다
    • level이 증가한다

레드블랙트리

  • 2-3-4 트리의 구조를 가지지만, 2개의 노드만 가지고 있다
    • 따라서 BST이다
    • 나머지 -3-4 영역은 Red 혹은 Black인지를 나타내는 encoded 이다
  • 성질
    • 루트 노드와 모든 리프노드는 블랙이다
    • 레드 노드의 자식은 언제나 블랙이다
    • 오직 블랙 노드만이 레드 노드의 부모가 될 수 있다
    • 노드는 블랙 또는 레드이다
  • 루트 노드로부터 말단 노드까지 도착하는 경로에는, 말단 노드를 제외하면 같은 수의 블랙 노드가 있다
  • 루트 노드부터 가장 먼 경로까지의 거리가, 가장 가까운 경로까지의 거리의 두 배보다 항상 작다.
    • 다시 말해 레드블랙 트리는 개략적으로 균형이 잡혀있다.
  • 삽입, 삭제, 검색 시 최악의 경우(worst-case)에서의 시간복잡도가 트리의 높이(깊이)에 따라 결정되기 때문에 보통의 이진검색 트리에 비해 효율적
    • 최악의 경우에도 일정한 실행 시간을 보장
    • AVL은 레드 블랙 트리보다 더 엄격하게 균형이 잡혀 있기 때문에 더 많은 회전이 필요

Treversal

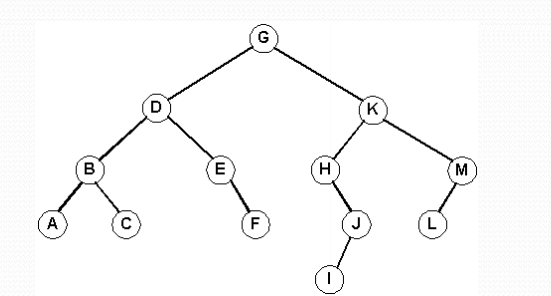
post_thumbnail

inorder traversal

  • traverse left → visit → traverse right
  • A B C D E F G H I J K L M

preorder traversal

  • visit → traverse left → traverse right
  • G D B A C E F K H J I M L

postorder traversal

  • traverse left → traverse right → visit
  • A C B F E D I J H L M K G

맵 map & 셋 set

  • 맵은 key와 value를 동시에 저장
    • 존재하지 않는 key와 value를 []를 사용해 추가 가능
    • 존재하지 않는 key로 탐색을 시도하면, 디폴트 생성자를 호출
  • 셋은 value 자체만 저장
  • 레드블랙트리 구조를 이용
  • 검색이 빨라야 하고 정렬이 필요한 자료를 저장할 때 사용
    • 메모리에 접근할 때 O(log n)의 시간이 소요
      • 바이너리 트리의 searching algorithm time complexity O(log n)
    • 값을 찾기 위해 탐색하는 비교 횟수는 트리의 높이에 비례

커스텀 클래스의 map과 set

  • 사용자 정의의 클래스를 map과 set에 넣고 싶다면 operator< 를 정의해야 함
  • strict weak ordering를 만족하는 operator < 를 디자인
    • A < A 는 거짓
    • (A < B) != (B < A)
    • A < B 이고 B < C 이면 A < C
    • A == B 이면 A < B 와 B < A 둘 다 거짓
    • A == B 이고 B == C 이면 A == C
  • 위의 조건을 만족하지 않는 오퍼레이터로 구동한다면 컴파일 에러는 없을지 몰라도, 런타임 에러가 발생할 가능성

멀티맵 multimap vs. 멀티셋 multiset

// 아래와 같은 경우에는 [] 오퍼레이터로 값을 불러올 수 없음
// 키에 중복되는 값 중 어떤 값을 불러와야 할지 모르기 때문
int main() {
  std::multimap<int, std::string> m;
  m.insert(std::make_pair(1, "hello"));
  m.insert(std::make_pair(1, "hi"));
  m.insert(std::make_pair(1, "ahihi"));
  m.insert(std::make_pair(2, "bye"));
  m.insert(std::make_pair(2, "baba"));
}

// find 함수는 존재
// 해당 키가 없다면 end() 를 반환
// 키가 있다면 해당하는 값 중 '아무거나' 반환
std::cout << m.find(1)->second << std::endl;

// 1 을 키로 가지는 반복자들의 시작과 끝을
// std::pair 로 만들어서 리턴한다:
// 
// 1 : hello 
// 1 : hi 
// 1 : ahihi 
auto range = m.equal_range(1);
for (auto itr = range.first; itr != range.second; ++itr) {
  std::cout << itr->first << " : " << itr->second << " " << std::endl;
}

해시테이블 hashtable

  • 충분히 적은 양의 데이터를 저장하고 빠른 검색
  • O(1) 검색을 지향
  • Linear Probing과 Chaining을 이용해 Collision을 resolve
  • overhead 발생 가능성

Linear Probing (open addressing)

  • 해당 slot이 occupied면 다음 unoccupied slot에 저장 (방향은 중요하지 않음)
  • Open addressing 중에 하나
  • Chaining보다 더 적은 메모리를 사용
  • 모든 데이터가 하나의 slot안에 따로 저장됨
  • slot이 꽉차면 더 이상 저장할 수 없음

Chaining

  • 각 슬롯이 list 구조로 되어 있음
  • 같은 key를 공유하는 value들이 한 slot 안에 list 구조로 여러 개 저장
  • 위의 방법은 모두 mostly O(1)이지만, 특별한 경우에 linear sequence를 통한 시간 소요가 발생할 수도 있다

출처

Categories: ,

Updated: