Juyong Jeong

Juyong Jeong

💻Game Client Programmer

Sorting의 종류

Bubble Sort

post_thumbnail

void bubble_sort(vector<int>& v)
{
	int size = static_cast<int>(v.size());

	for (int i = 0; i < size - 1; ++i)
	{
		bool swapped = false;

		// 매번 탐색한 범위에서 가장 큰 element를 맨 뒤로 밀어냄
		// => 비교할 범위를 줄임
		for (int j = 0; j < size - i - 1; ++j)
		{
			if (v[j] > v[j + 1])
			{
				swapped = true;
				swap(v[j], v[j + 1]);
			}
		}
		
		// done sorting
		if (!swapped)
			break;
	}
}

Selection Sort

post_thumbnail

void selection_sort(vector<int>& v)
{
	// 탐색한 범위 중 가장 작은 element를 맨 앞으로 보냄
	int size = static_cast<int>(v.size());

	for (int i = 0; i < size - 1; ++i)
	{
		int min = i;
		// 가장 작은 원소의 index 찾음
		for (int j = i; j < size; ++j)
		{
			if (v[min] > v[j])
				min = j;
		}

		// 맨 앞서부터 가장 작은 원소의 index와 swap
		if (min != i)
			swap(v[min], v[i]);
	}
}

Insertion Sort

post_thumbnail

// 가상의 sorted와 unsorted로 구간을 나누어 정렬
void insertion_sort(vector<int>& v)
{
	int size = static_cast<int>(v.size());

	for (int i = 1; i < size ; ++i)
	{
		// 선택한 원소가 적정 위치에 갈 때까지 체크하고 swap
		for (int j = i ; j > 0; --j)
		{
			if (v[j] < v[j - 1])
				swap(v[j], v[j - 1]);
		}

		// 비교가 끝나면 다음 i로 옮겨 반복...
	}
}

Merge Sort

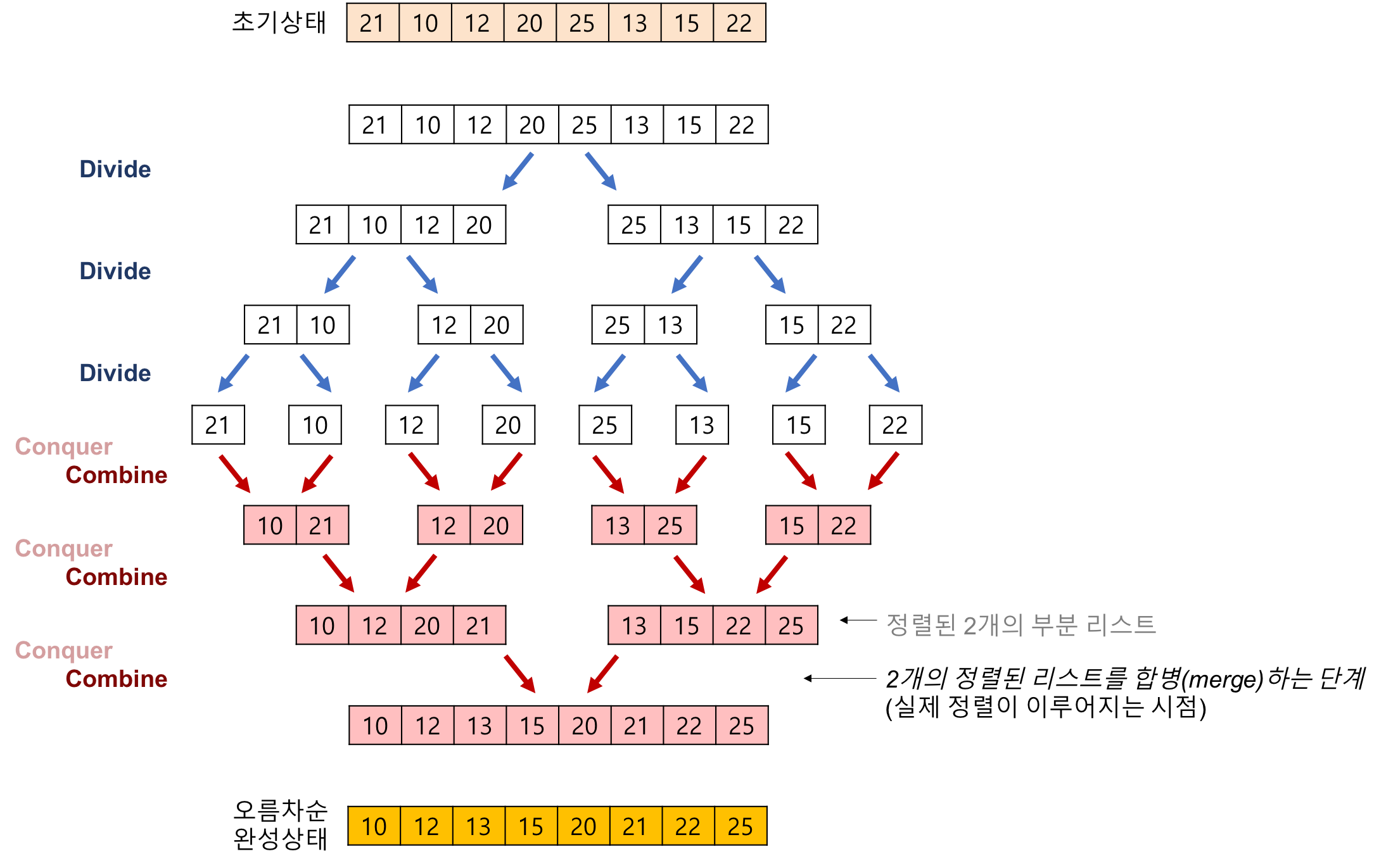
post_thumbnail

// divide를 먼저 실행한 뒤 -> conquer하는 과정에 sorting
void merge_sort(vector<int>& v, int l, int r)
{
	if (l < r)
	{
		int mid = (l + r) / 2;

		// divide
		merge_sort(v, l, mid);
		merge_sort(v, mid + 1, r);

		// conquer
		int i = 0, j = 0, k = l,
			n1 = mid - l, n2 = r - (mid + 1);

		// 두 갈래로 나누어 복사
		vector<int> left(v.begin() + l, v.begin() + mid + 1),
			right(v.begin() + mid + 1, v.begin() + r + 1);

		// left와 right의 원소를 순서대로 비교하며 배열 v로 값 복사
		while (i <= n1 && j <= n2)
		{
			if (left[i] < right[j])
				v[k++] = left[i++];

			else
				v[k++] = right[j++];
		}

		// 위 과정에서 한쪽 배열이 먼저 끝날 경우,
		// 나머지 배열을 복사
		while (i <= n1)
			v[k++] = left[i++];

		while (j <= n2)
			v[k++] = right[j++];
	}
}

Quick Sort

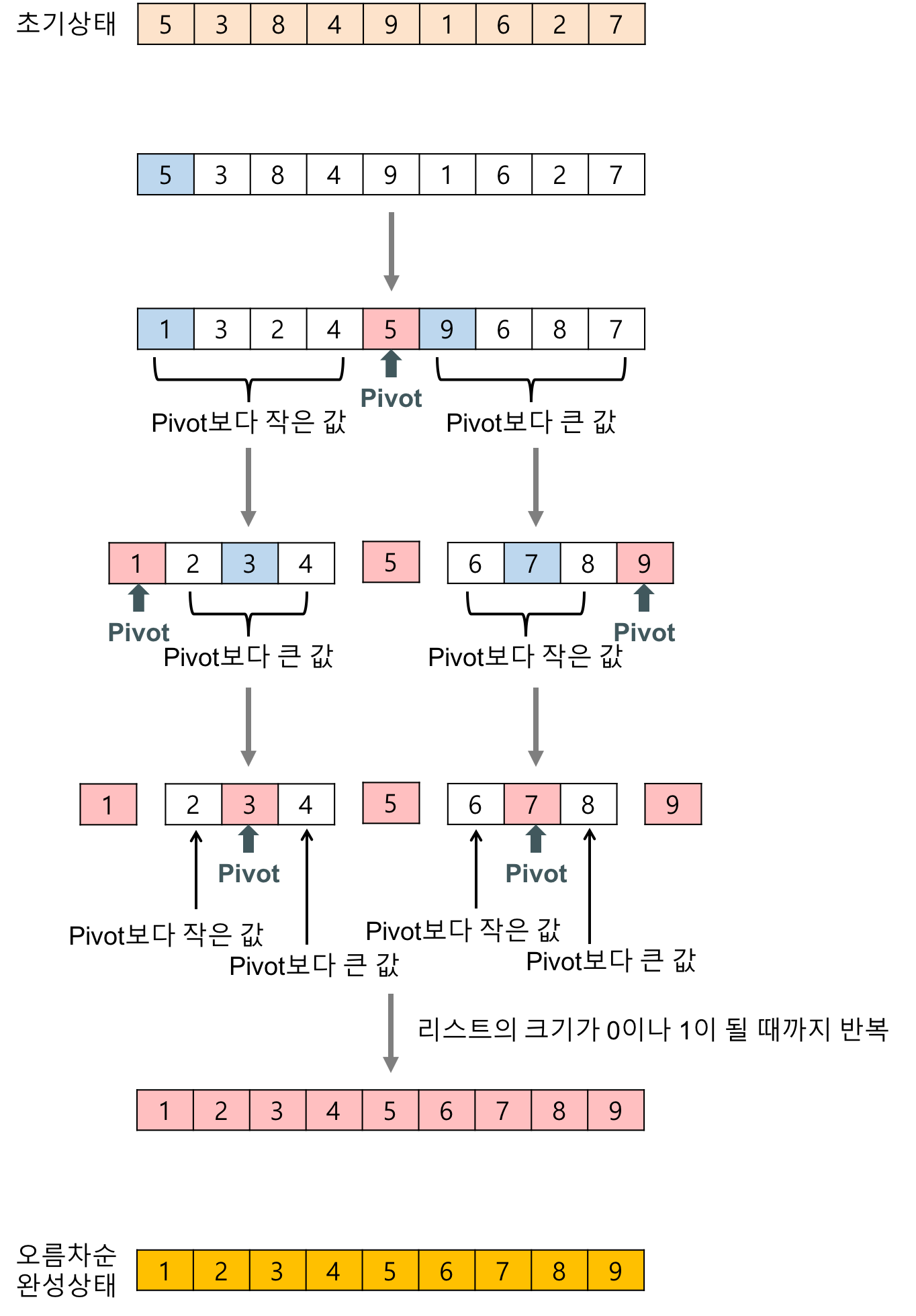
post_thumbnail

// divide 하는 과정에서 pivot을 기준으로 swap을 통해 sorting
void quick_sort(vector<int>& v, int l, int r)
{
	int i = l, j = r;
	// 축을 정하고 그를 기점으로 swap
	int mid = v[(l + r) / 2];

	while (i <= j)
	{
		while (v[i] < mid)
			++i;

		while (mid < v[j])
			--j;

		if (i <= j)
		{
			swap(v[i], v[j]);
			++i, --j;
		}
	}

	if (l < j) quick_sort(v, l, j);
	if (i < r) quick_sort(v, i, r);
}

Locality (지역성)

  • CPU가 짧은 시간 범위 내에 일정 구간의 메모리 영역을 반복적으로 엑세스하는 경향
    • 메모리 정보를 균일하게 엑세스 하는 것이 아님
    • 짧은 시간 내에 특정 부분을 집중적으로 참조
  • 함수 설계 및 사용처를 보고 특정 메모리를 캐시에 올려 재사용할 수 있음
    • 현재 프로세스의 실행 패턴을 보고 가까운 미래에 프로세스의 코드와 데이터를 합리적으로 사용하도록 예측
    • 자주 사용되는 페이지를 물리 메모리와 캐시 메모리에 둠
  • 지역성의 정도가 떨어지면 캐시에 접근하지 않고 메인 메모리로 접근
    • = 캐시 미스

quick sort vs. merge sort

merge sort post_thumbnail

quick sort post_thumbnail

  • merge sort는 정렬할 전 구간에 걸쳐 엑세스
  • quick sort는 divide한 구간을 차례로 반복적으로 엑세스
  • 참조의 지역성
    • 대부분의 프로그램들은 모두 단시간에 반복적으로 접근하는 데이터가 존재
    • 이 과정을 효율적으로 수행하기 위해 캐시 사용
  • quick sort이 merge sort보다 더 참조의 지역성 성질을 띰
    • 캐시의 도움을 더 받음

Quick Sort의 Worst Case

  • Quick sort는 피벗을 기준으로 left와 right로 divide 하는 로직
  • divide를 총 원소의 개수만큼 하는 경우
    • 이미 정렬이 되어있는 경우

Radix Sort 기수 정렬

post_thumbnail

  • 낮은 자리 수(digit) 부터 정렬하는 알고리즘
  • 비교 연산을 하지 않고, 정렬 속도가 빠르나 메모리가 더 많이 필요함
  • 시간 복잡도는 O(dn)
  • 자리수가 고정되어 있어서 안정성이 있는 정렬 방식
void radix_sort(int array[], int size){

	vector<queue<int>> queues;
	queues.emplace_back(10);

	int max = array[0];
	int digit = 0;
	int factor = 1;

	// 최대 자리수 계산
	for(int i=1; i<size; i++)
	{
		if(max<array[i]) 
			max = array[i];
	}
	for(int i=max; i>0;i/=10)
	{
		digit++;
	}

	// 정렬해야할 원소 중 최대 자리수까지 반복
	for(int i =0; i<digit; i++)
	{
		// 0~9까지 돌아가며 반복
		for(int j=0; j<10; j++) 
		{ 
			// 원소들을 돌아가며 반복
			for(int k=0; k<size; k++)
			{
				// 자리수가 동일한 원소를 찾으면 put
				if((array[k] / factor) % 10 == j)
				{
					q[j].push(array[k]);
				}
			}
		}
		factor *=10;

		// 자리수 별 queue에 들어가 있는 원소들을 차례대로 정렬
		for (auto& q: queues)
		{
			int qSize = q.size();
			for(int i=0; i < qSize; i++){
				array[i] = q.pop();
			}
		}
	}
}

Shell Sorting 쉘 정렬

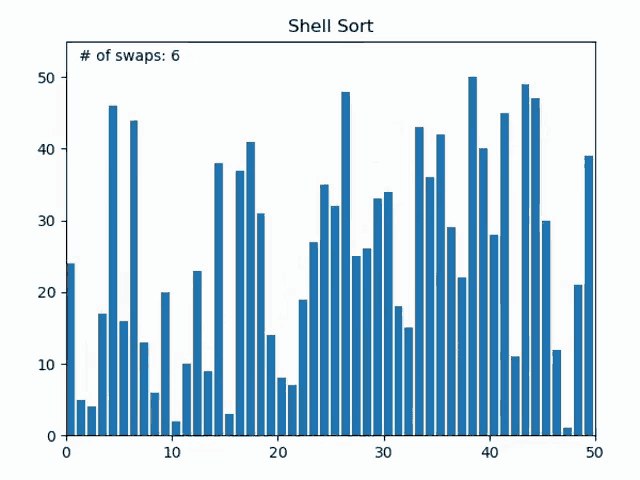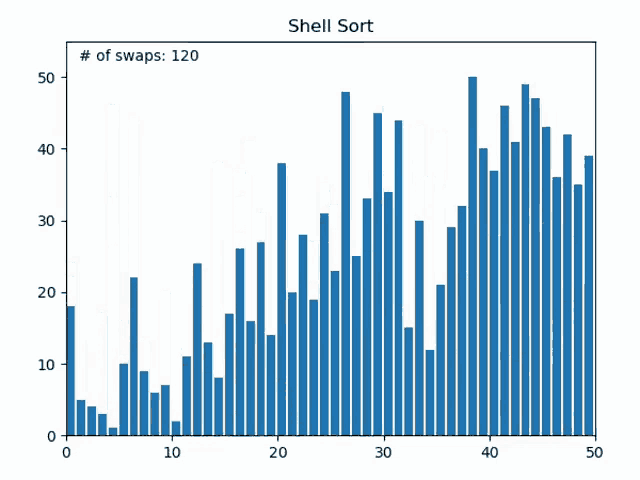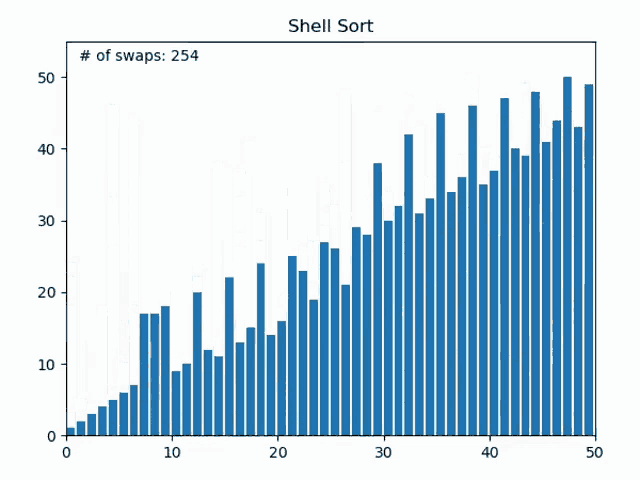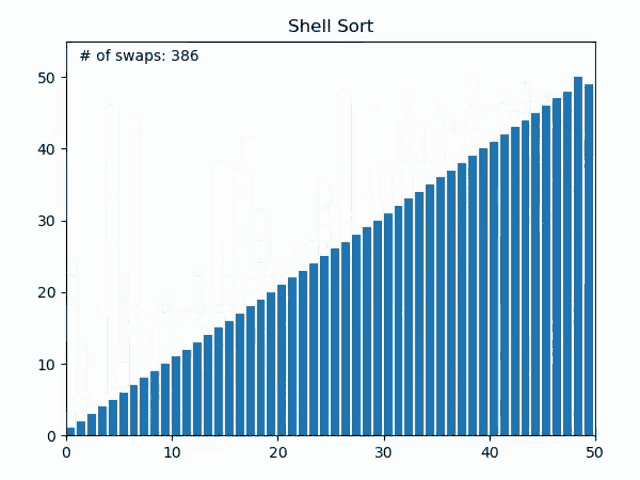
post_thumbnail

  • Insertion Sorting의 확장 버전
  • Insertion이 이웃한 원소끼리 비교를 하는데 비해, Shell은 일정 간격끼리 비교
  • 시간 복잡도는 O(n)
    • 평균의 경우 O(n^1.5)
    • 최악의 경우 O(n^2)
void shell_sort(int a[], int size) {
    int i, j, temp;

	// 간격 세팅
    int gap = size / 2;

    while( gap > 0 ) {
        for( i=gap; i<size; i++ ) {

			temp = a[i];
            j = i;
			// 일정 간격뒤에 떨어진 원소와 비교
            while( j>=gap && a[j-gap]>temp ) {
				// 앞쪽 원소가 더 크다면 swap
                a[j] = a[j-gap];
                j -= gap;
            }
            a[j] = temp;
        }
		// 더 작은 간격으로 gap 업데이트
        gap /= 2;
    }
}

int main() {
    int arr[] = {9,1,22,4,0,-1,1,22,100,10};
    int size = sizeof(arr)/sizeof(int);
    shell_sort(arr, size);
    for(int x: arr) std::cout << x << " ";
    // -1 0 1 1 4 9 10 22 22 100 
}

Heap Sorting 힙 정렬

post_thumbnail

  • 최소 힙 또는 최대 힙을 구현해 정렬
  • 최대, 혹은 최소 값을 차례대로 삭제하면서 pop 되는 원소들을 차례대로 정렬
  • 힙 설명

정렬 별 장단점

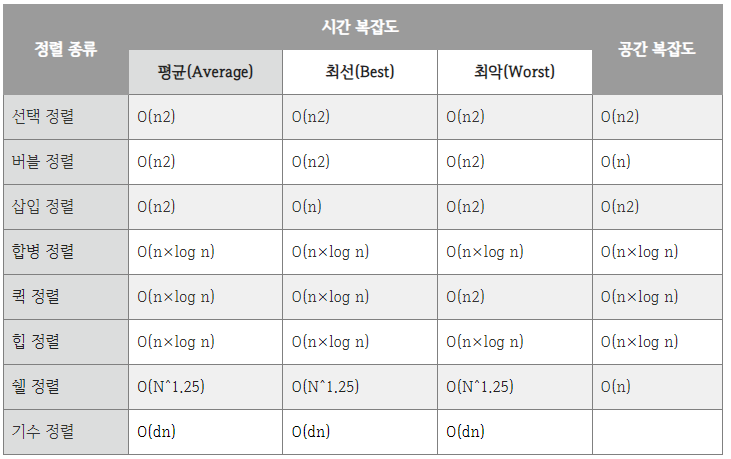
post_thumbnail

정렬 별 시간 / 공간 복잡도

post_thumbnail

출처

Categories: ,

Updated: