벡터의 한계
- 어떤 물체를 화면에 표현하려면 벡터만으로는 부족
- 벡터는 크기와 방향 성분만을 가짐
- 위치 정보가 필요
- 위치는 무엇으로 표현하는가?
아핀 공간
- 점이 존재하는 공간
- 유클리드 공간은 벡터 공간이 아니라 아핀 공간
- 백터 공간으로 통용되는 이유는 아핀 공간을 통해서 벡터 공간을 형성할 수 있기 때문
- 아핀 공간의 정의 = 점들의 집합 + 하나의 벡터 공간
점과 벡터
아핀 공간 정의
- V라는 벡터 공간이 있고, V 위에 아핀 공간을 A라는 점들의 집합으로 정의
- V와 A 사이에 대응이 존재하고 세가지 성질을 만족
대응
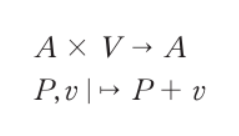
- A의 점과 V의 벡터로 연산을 했을 때 결과는 점이다
- 하나의 점과 하나의 벡터의 짝은 하나의 덧셈 연산으로만 대응된다
조건
- 아핀 공간에서의 점과 벡터의 덧셈은 벡터와 벡터의 덧셈 연산과 동일하다
- 점과 벡터의 x, y, z 성분을 모두 더한 것과 같다
- 따라서 이를 수식화할 때는 반드시 점인지 벡터인지 명확하게 표기하여야 한다
- A에 속한 모든 점 P에 대해 영벡터를 덧셈하면 P이다
- 영벡터는 벡터 공간 V의 덧셈에 대한 항등원이다
- A에 속한 모든 점 P와 V에 속한 임의의 벡터 v, w에 대해 P + (v + w) = (P + v) + w가 성립한다
- A에 속한 점 P, Q가 있을 때 P + v = Q를 만족하는 단 하나의 벡터 v가 존재한다
점과 벡터의 연산
- 벡터 ± 벡터 = 벡터
- 점 ± 벡터 = 점
- 점 - 점 = 벡터
