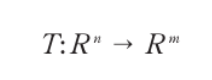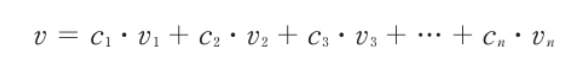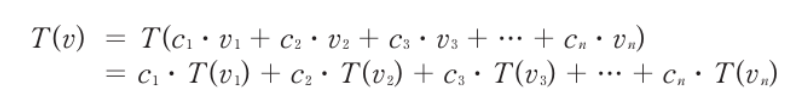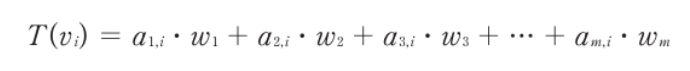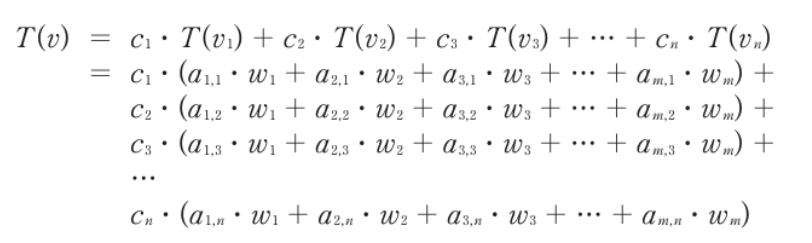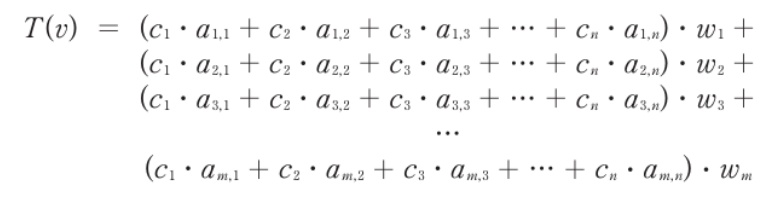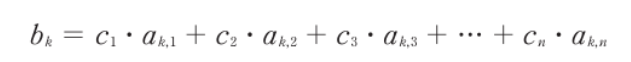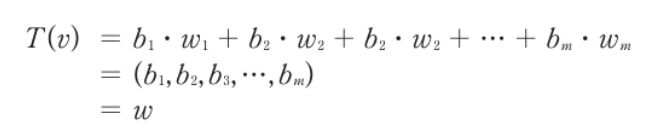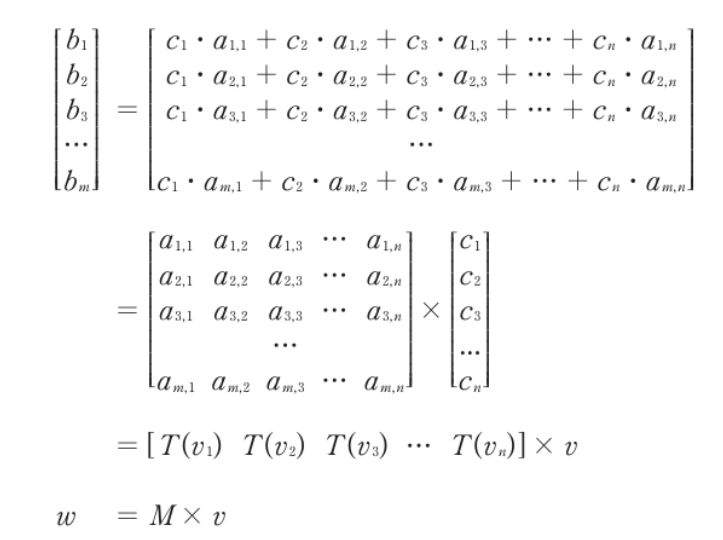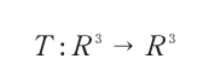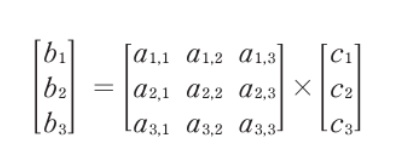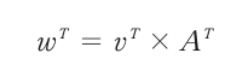Linear Transformation (1)

선형 변환과 행렬

• 선형 변환이란
  • 하나의 벡터 공간을 다른 벡터 공간으로 변환하는 함수
  • 선형 변환을 정의하는 두 특성이 변환 후에도 벡터 공간의 조건을 그대로 만족하기 때문

선형 변환과 행렬

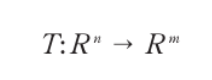
• 선형 변환 T를 통해 벡터 공간 V를 W로 변환
  • 공간 V의 기저 벡터로 공간 W의 벡터를 표현할 수 있다
  • V는 W를 확장 span 했고, W의 기저 basis이다

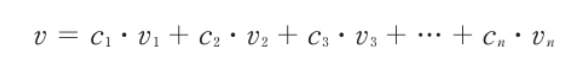
• 공간 V의 벡터 중 하나의 v는 위와 같이 표현할 수 있다

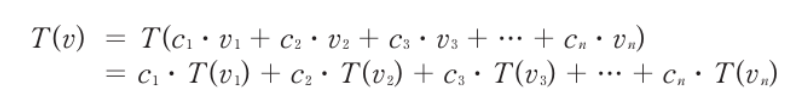
• 선형 변환 T를 적용한 벡터 v는 위와 같이 표현한다
  • 선형 변환의 특징을 적용한 것이다
• 선형 변환을 수행할 때,
  1. 기저 벡터들을 먼저 선형 변환한다
     • v_n -> T(v_n)
  2. 이 다음, 변환하고자 하는 벡터의 선형 조합에 쓰이는 스칼라 값들과 새롭게 변환된 기저 벡터들과의 선형 조합을 한다
     • c_1 * T(v_1) + c_2 * T(v_2) + … + c_n * T(v_n)

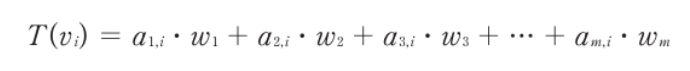
• 선형 변환된 공간 W의 벡터들을 w_n으로 표현할 수 있다
• 이 벡터들과 임의의 스칼라 값을 이용해 선형 조합을 할 수 있다
• 위의 식의 각 벡터들은 공간 W의 기저 벡터들이다

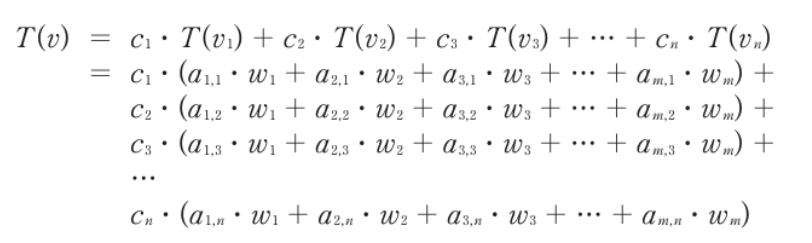
• 각 a_(i, j) * w_k를 풀면 위와 같다
• 스칼라 a에 첨자를 붙인다
  • 몇번째 기저벡터를 대상으로 하는 선형변환인지 알수 있다
  • 나중에 행렬로 표현하기에도 용이하다

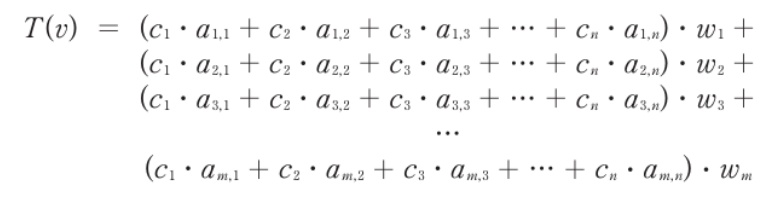
• 위의 식은 W의 기저벡터 w로 다시 전개한 것이다

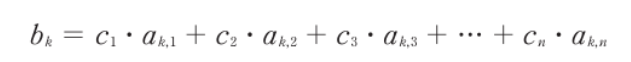
• b_k를 정의하여 위와 같이 축약한다
• b_k는 스칼라 값 a_k를 통해 선형 변형된 스칼라 c_k 값의 결과이다

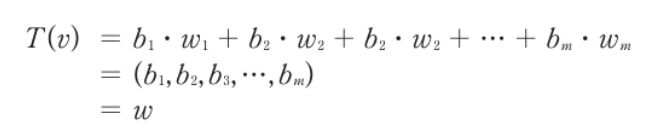
• 표준 기저 w_1, w_2, …, w_n은 표시하지 않는다

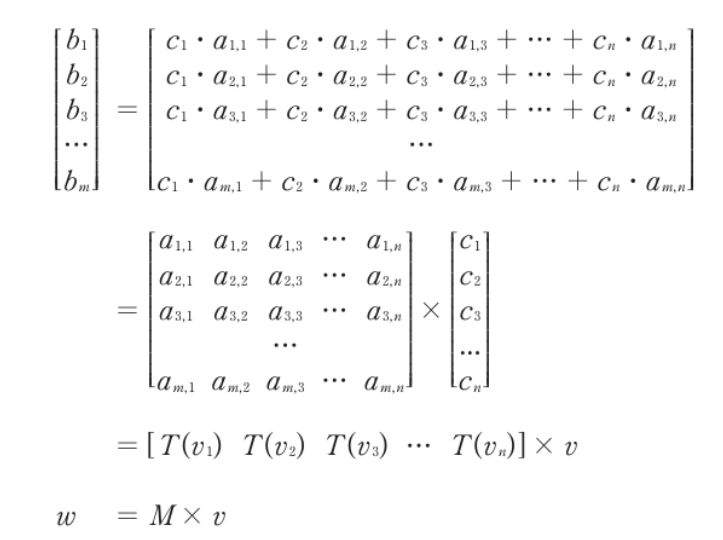
• 최종적으로 선형 변환된 벡터 w
• 이제 맨 오른쪽의 열벡터 v는 변환하고자 하는 열벡터이다
• M은 확대행렬이다
  1. 선형 변환 T를 적용해 공간 V의 v 벡터들을 변환한 값들이다
  2. 이들을 열벡터로 만들어 이어 붙인 것이다
• 모든 선형변환은 행렬로 변환이 가능하다

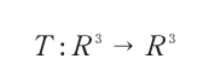
• 그래픽스를 위해 사용하는 3차원 공간에서의 선형변환 T는 위와 같다

• 행렬 M은 3 x 3 정방 행렬이다

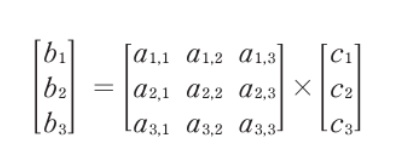
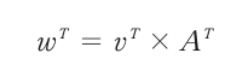
• DirectX를 사용하는 경우 전치 행렬로 위와 같이 변환한다