Linear Transformation (2)
크기 변환
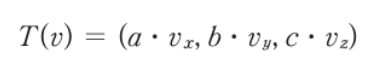
- 벡터의 크기와 방향 중 크기만 변경하는 것
- 각 성분에 각 계수만큼의 크기를 곱해 양을 바꿈
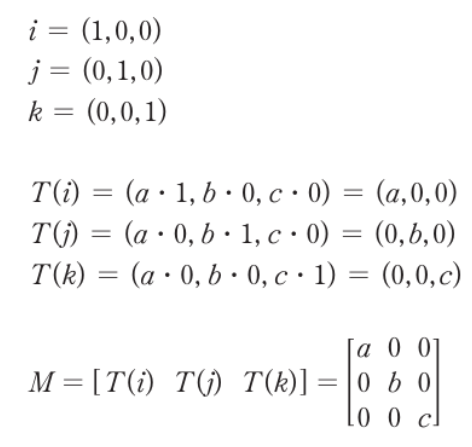
- 각 기저벡터에 대해 주대각성분 a, b, c 만큼의 양을 곱한 변환행렬
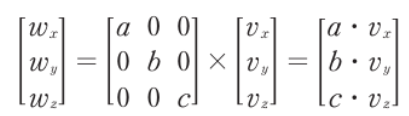
- 행렬 곱셈은 위와 같다
- a, b, c가 모두 값이 같으면 모든 축에 대해 동일 비율로 크기를 변환하는 것이다
- 이를 균등 크기 변환 uniform scaling 혹은 isotropic scaling 이라 한다
- 크기가 다른 변환은 비균등 크기 변환 non-uniform scaling 혹은 anisotropic scaling이라 한다
크기 변환 역행렬
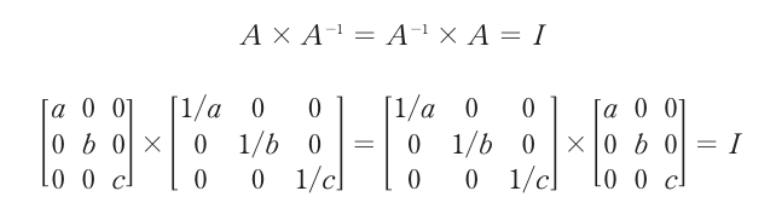
- a만큼 크기를 변환했으면, 1/a만큼 다시 변환시킨다
회전 변환
- 얼마나 회전할지, 회전의 양
- 무엇을 기준으로 회전할지, 회전의 축
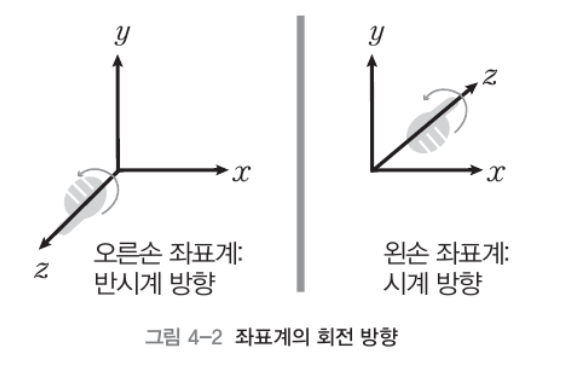
- 반시계, 시계 방향으로 회전할지의 결정 여부는 좌표계
좌표 축 기준 (z축 기준)
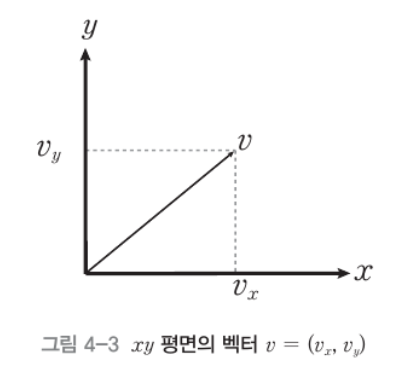
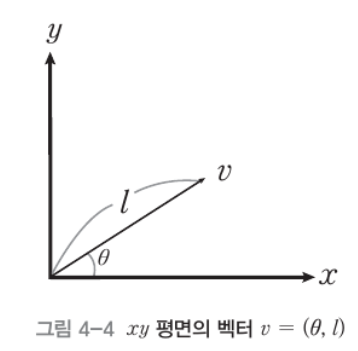
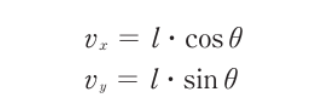
- 회전 축인 z축 성분에는 변화가 없다
- 극좌표계 polar coordinate를 통해 위와 같은 연관 식이 성립한다
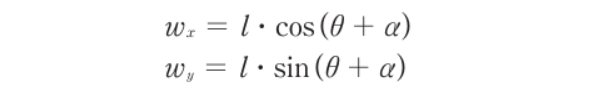
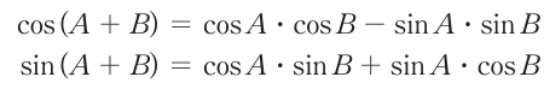
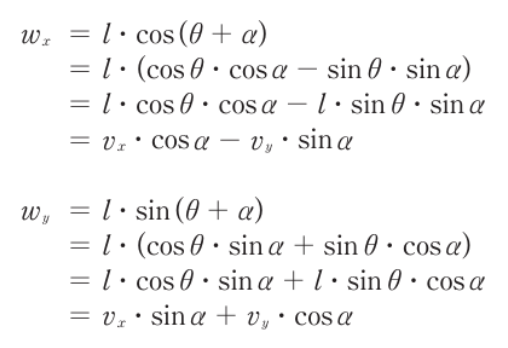
- 벡터의 극좌표계 표현식과 삼각함수의 성질을 이용해 회전 변환 T를 구할 수 있다
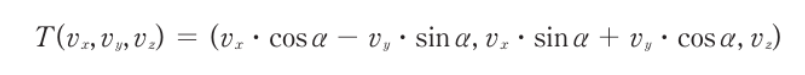
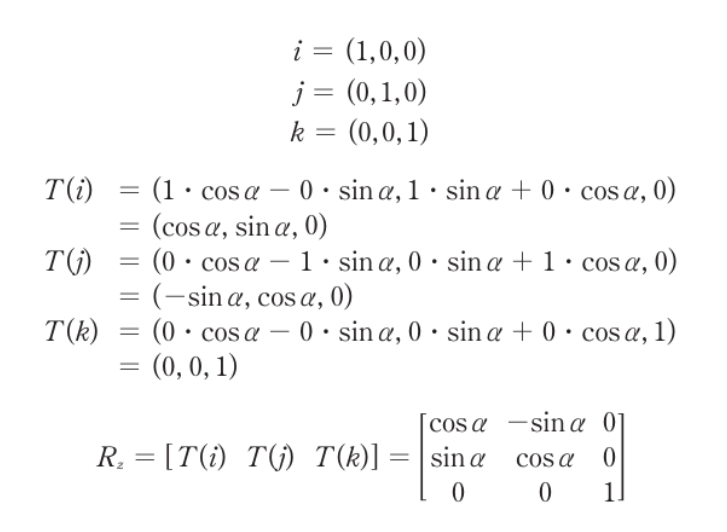
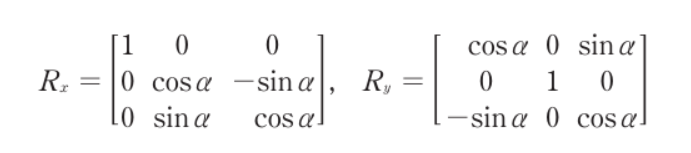
- 기저벡터 i,j,k를 두고 식을 간소화한 뒤 변환행렬을 위와 같이 구할 수 있다
- 같은 받법으로 x, y축에 대한 회전 행렬도 구할 수 있다
축 회전 변환 역행렬
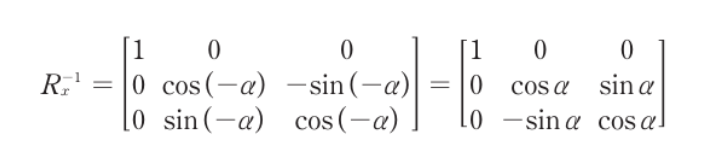
- x축에 대한 회전 행렬의 역행렬
- a만큼 회전했으면, 다시 -a만큼 회전시킨다
- 회전 변환 행렬이 직교 행렬이라는 점을 이용할 수도 있다
- 직교 행렬 - 행렬의 각 열/행벡터들이 서로 정규 직교
- 길이가 모두 1
- 상호 수직인 경우
- 직교 행렬의 역행렬은 그 행렬의 전치행렬과 같다
- 어떤 행렬의 행과 열을 뒤바꾸면 전치 행렬 transpose matrix라 한다
임의의 축 기준
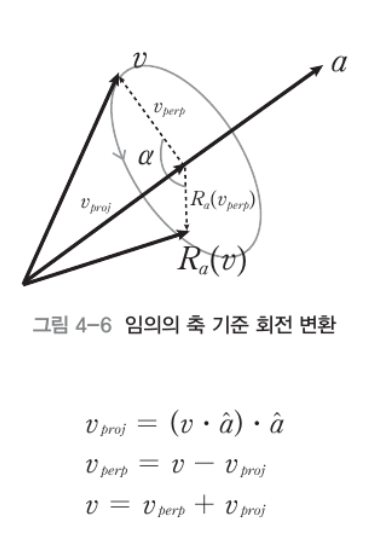
- 벡터 v를 축 a에 대해 degree a만큼 회전변환
- 벡터 a가 단위벡터인 경우의 위의 식이 성립
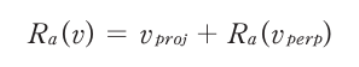
- 변환된 벡터 R_a(v)는 축의 단위벡터인 v_proj와 v_perp를 회전시킨 R_a(v_perp)의 합
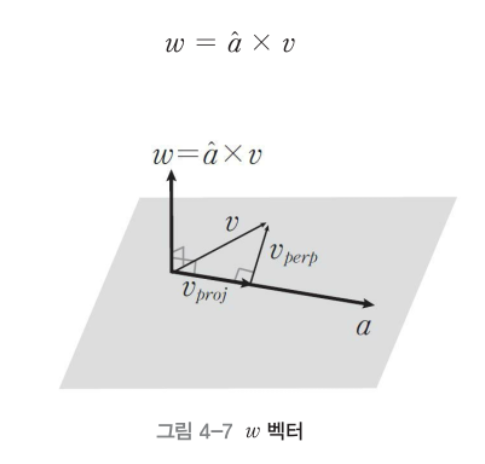
- 위의 그림을 통해서 벡터 w를 표현할 수 있다
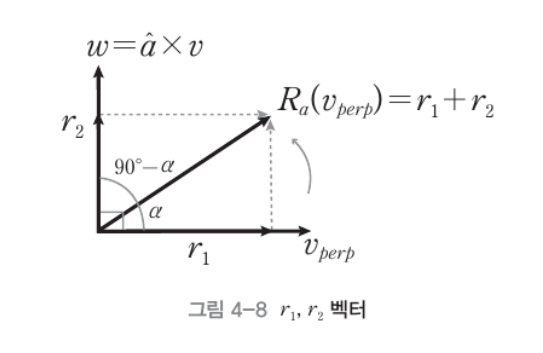
- w와 v_perp 두 축을 기준으로 평면 좌표를 새로 생성하면 위와 같이 표한할 수 있다
- r1과 r2 두 벡터를 구해보자
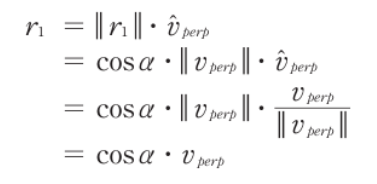
- r1의 길이는 위와 같이 표현가능하다
- R_a(v_perp)가 아닌 v_perp가 쓰인 이유는, 두 벡터는 상호 회전 변환만을 거쳤기 때문
- 즉, 길이가 같기 때문
- 그림 4-6 참조
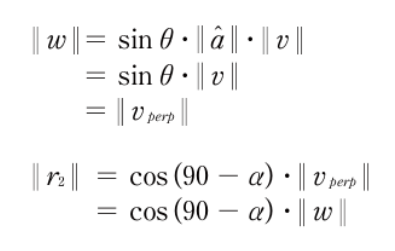
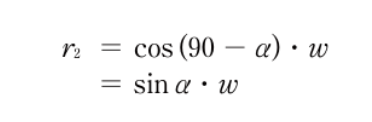
- r2 역시 위와 같이 구할 수 있다
- 벡터 w의 길이는 마찬가지의 이유로 v_perp와 그 길이가 같다
- 위의 식 표현은 그냥 역순으로 이해하는 게 속이 편하다
- 그림 4-7 참조
- R_a(v_perp)가 아닌 v_perp가 쓰인 이유는, 두 벡터는 상호 회전 변환만을 거쳤기 때문
- 마찬가지로 길이가 같기 때문
- v_perp 역시 w를 회전만 했으므로, 길이는 같다
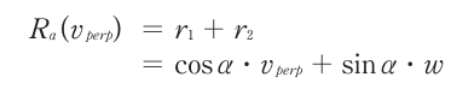
- 이제 R_a(v_perp)를 위와 같이 표현할 수 있다
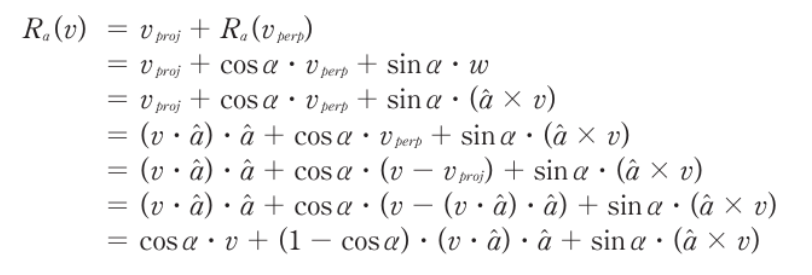
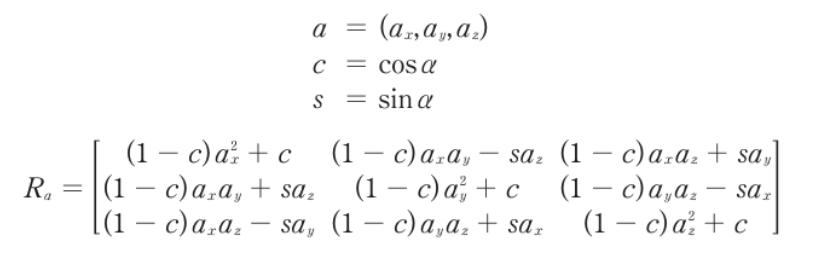
- 그리고 위의 푀종 식이 로드리게스 회전 공식 Rodrigues’ rotation formula라고 한다
- 아래 행렬은 임의의 축에 대한 회전 변환 행렬이다
- 여기는 나도 잘 모르겠다
- 선형 변환의 조합과 행렬곱셈도…