Matrix

행렬 Matrix

• m x n 행렬에서 m = n 이면 정방행렬 square matrix 이다
• 모든 요소가 0이면 영행렬 zeron matrix 이다
• 어떤 행렬의 행과 열을 뒤바꾸면 전치 행렬 transpose matrix라 한다
  • 전치한 행렬이 원래 행렬과 같다면 대칭 행렬 symmetric matrix라 한다
  • 주대각선상에 있는 성분들을 주대각성분 main diagonal 이라 한다
• 행렬의 곱셈 A x B 는 A의 열의 개수와 B의 행의 개수가 같아야 한다
  • 교환 법칙도 성립하지 않는다
  • (A x B)_T = B_T x A_T
• 정방 행렬들 사이의 곱셈의 경우 항등은 I가 존재한다
  • A x I = I x A = A
• 두 정방 행렬의 곱이 순서와 상관없이 항등원을 만들면 서로 역행렬이다
  • A^(-1) x A = A x A^(-1) = I
  • (A x B)^(-1) = B^(-1) x A^(-1)

선형계

• 행렬은 연립 1차 방정식을 푸는 것에서 시작된 개념
• 1차 방정식들만으로 구성된 것을 섢령방정식계 system of linear equations라 한다
  • 또는 선형계 linear system 이라 한다

가우스 소거법 Gauss elimination

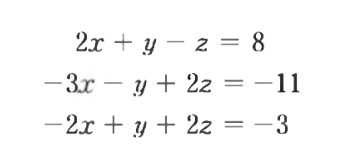
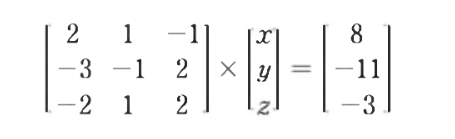
• 방정식을 각 계수 행렬 coefficient matrix와 상수 행렬로 치환한다
• 이후 전진 소거법과 후진 대입법을 차례로 적용하여 푼다

전진 소거법 Forward elimination

• 확대 행렬 augmented matrix로 치환한다
• 기본 행 연산 elementary row operation을 이용해 사다리꼴 형 row echelon form으로 반드는 방법이다
  • 사다리꼴 형이란, 주대각성분들은 모두 1이 되고 그 아래 성분들을 모두 0으로 만든 것이다
  • 선두 계수 pivot를 모두 1로 만드는 것이다

후진 대입법 Backward substitution

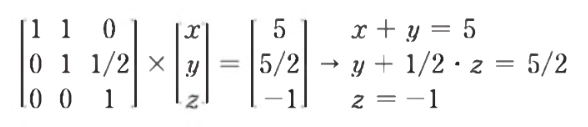
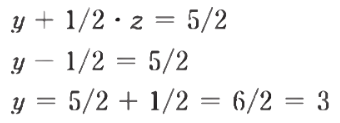
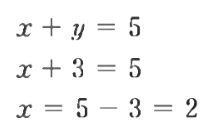
• 가장 아래의 행부터 값을 찾아 나가는 방식이다

가우스 요르단 소거법 Gauss-Jordan 티imination

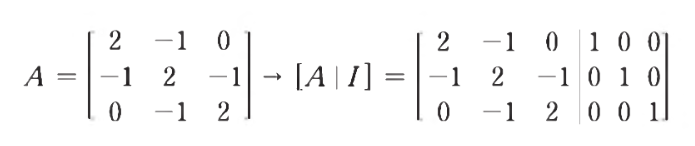
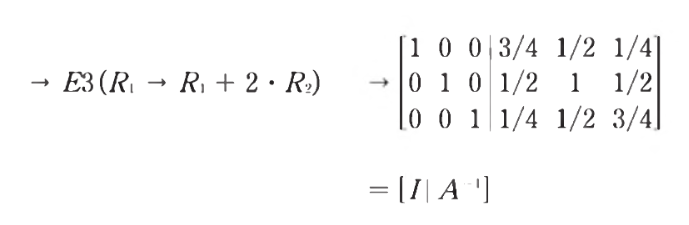
• 계수 행렬을 기약 행수 사다리꼴 형 reduced row echelon form으로 만드는 것이다
  • 선두 계수를 제외한 모든 성분이 0인 행렬
• 이는 역행렬을 구하는 데 사용된다
  • 한족을 I로 만들고 다른 한 쪽을 역행렬도 만드는 과정이다

행렬식 Determinant과 역행렬

• 라플라스 전개 Laplace’s expansion를 통해서 소행렬식을 전개하여 행렬식을 구하는 방법이다

• 크레이머 공식 Cramer’s rule은 가우스-요르단 소거법 보다 훨씬 빠르게 역행렬을 구할 수 있다
  
  

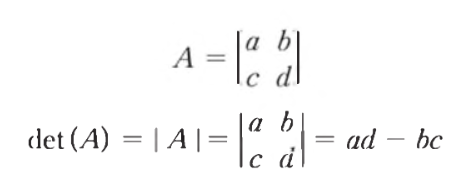
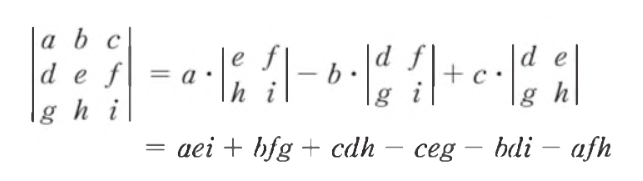
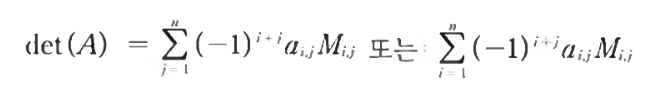
• 위는 정방 행렬의 행렬식 determinant를 구하는 방법
• 소행렬식 minor determinant
  • 식에서 단일 성분을 제외한 나머지 행렬의 행렬식
• 여인수 cofactor
  • 식에서 행렬식 앞의 계수

수반 행렬 adjugate matrix

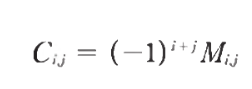
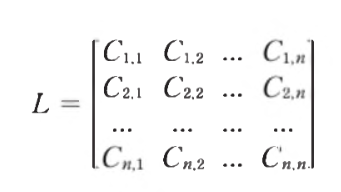
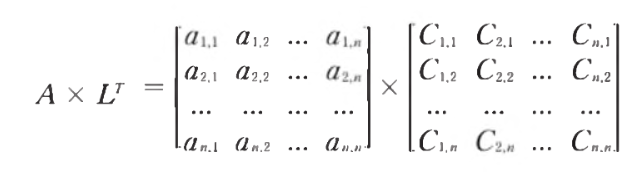
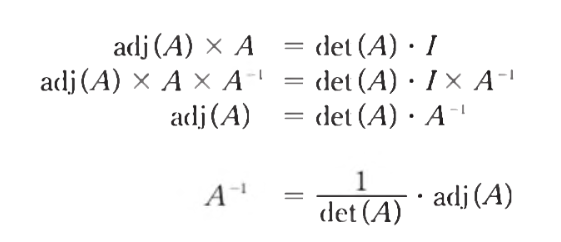
• C(i,j)는 여인수이다
• 행렬 L은 행렬 성분에 대응하는 여인수들을 모은 행렬이다
• L_T를 A의 수반행렬이라 한다
  • 교환 법칙이 성립한다
• 수반 행렬을 이용해 역행렬을 구할 수 있다

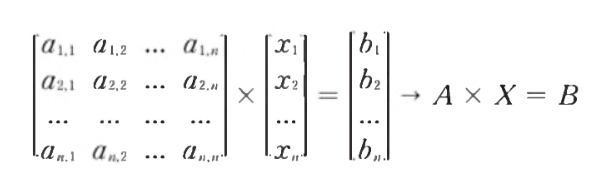
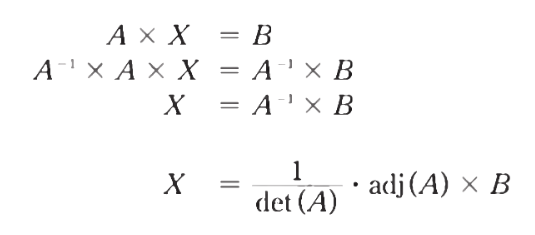
• 이는 선형계의 해를 구하는 방법이기도 하다
• det(A)는 0 이어서는 안된다

벡터와 행렬

• 벡터를 1개의 열로 표현하면 열 벡터 column-major vector
  • 일반 수학, OpenGL 등
• 벡터를 1개의 행으로 표현하면 행 벡터 row-major vector
  • Direct X 등

벡터 내적

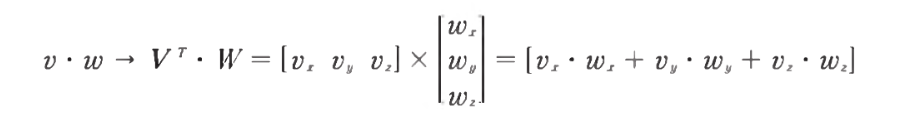
• 앞 행렬을 전치 행렬로 바꾸고 곱하면 된다

벡터 외적

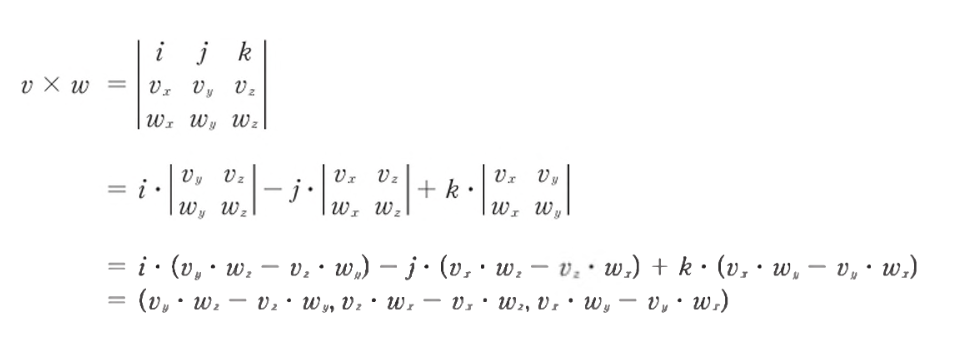
• 첫 번째 방법은 행렬식 그대로 연산하는 것이다

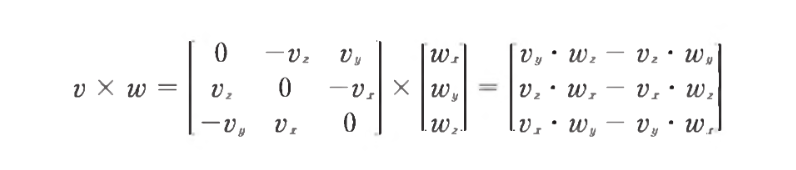
• 두 번째 방법은 반대칭 행렬 skew-symmetric matrix를 만드는 것이다
  • 주대각선을 기준으로 나머지 성분들을 대칭 시킨다
  • 기호는 반대이다
  • 나머지 벡터를 열벡터로 만들고 곱셈한다

벡터 투영

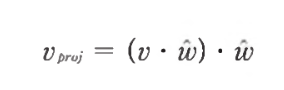
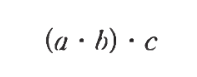
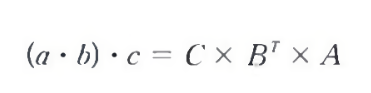
• 벡터 투영 식을 위의 행렬 연산으로 치환할 수 있다

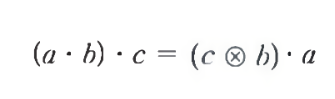
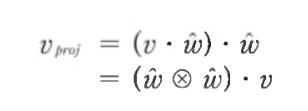
• 이때 행렬 C와 B^(T)를 곱하는 연산을 텐서곱 tensor product라 한다
• 텐서곱을 이용해 투영 벡터를 위와 같이 구할 수 있다

스칼라 삼중곱

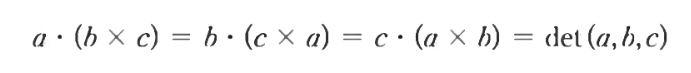
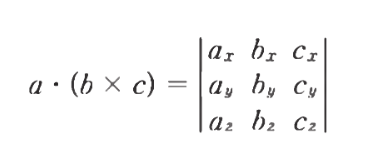
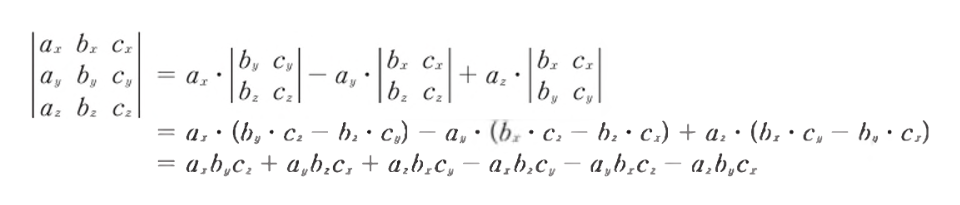
• 스칼라 삼중곱을 라플라스 전개를 사용한 행력식을 통해 구할 수 있다
• 이는 세 벡터가 이루는 평행육면체의 부피를 의미한다
  • 즉 행력식의 절대값이 부피가 된다는 뜻이다

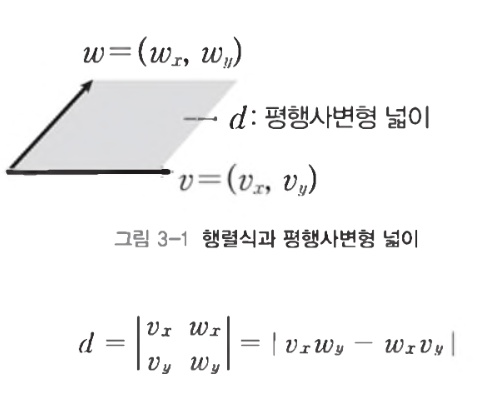
• 2차원일 경우는 넓이가 된다