[Math] Vector
유클리드 공간
- 임의의 점과 다른 한 점을 연결하는 직선은 단 하나다
- 임의의 선분은 양 끝으로 얼마든지 연장할 수 있다
- 임의의 점을 중심으로 하고 임의의 길이를 반지름으로 하는 원을 그릴 수 있다
- R은 실수로 이루어진, R^2은 2차원 공간, R^3는 3차원 공간을 의미
3차원 공간에서의 벡터
- 3차원 공간은 엄밀히 아핀 Affine 공간
- 벡터만 있는 것이 아니라 점이 같이 있다
- 벡터는 위치 개념이 없고 길이와 방향이 같으면 어디에 있든 같은 벡터다
- 길이가 0인 벡터는 영 벡터 또는 Null 벡터라고 한다
선형 조합과 기저
- 어떤 벡터들의 집합 S = {v_1, v_2, v_3, …, v_n }이 있다
- 어떤 벡터 v = s_1 * v_1 + s_2 * v_2 + … + s_n * v_n 로 선형조합을 나타낼 수 있다
- s_x 들은 임의의 스칼라 값들이다
- 선형 조합이란 집합 각각의 원소에 임의의 스칼라 값들을 곱한 후 모두 더한 것을 말한다
- 임의의 스칼라 값을 사용하기 때문에 무수히 많은 선형 조합이 있다
- S로 가능한 모든 선형 조합들로 생겨난 결과들을 다시 집합으로 묶은 벡터 공간 T를 정의한다.
- 이때 벡터 공간 S는 공간 T를 확장 span 한다
- 또 이때 S의 한 원소가 나머지 원소들의 선형 조합으로 만들어질 수 없다면 S를 T의 기저 basis 라고 한다
- 이를 S의 원소들이 서로에 대해 선형 독립 Linear Independent라고 한다
- 어떤 v도 v_1, v_2, …, v_n들의 선형 조합으로 생성이 불가능하다는 의미다.
예시
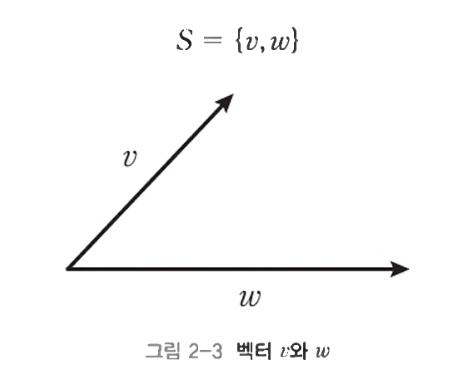
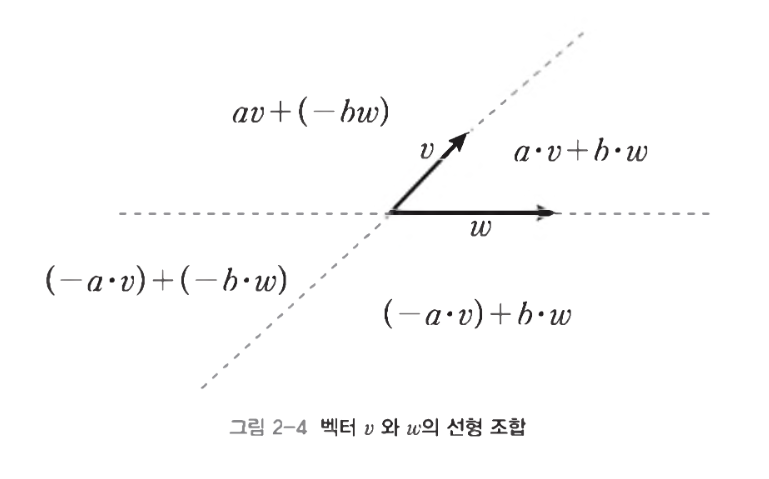
- 위의 두 벡터로, 2차원 상의 모든 벡터가 표현된다
- v와 w는 서로 어떤 스칼라 곱을 통해서도 동일한 벡터가 될 수 없다
- 둘은 서로 선형 독립이다 * 1과 2의 조건을 통해 S = {v, w}는 R^2를 생성하는 기저이다 * 각 v, w는 기저 벡터이다
표준 기저
- 각 직교 좌표계 축의 양으 방향을 가리키는 기저 벡터
- 흔히 각 i, j, k로 칭한다
- 보통 다음과 같이 표현한다
- v = v_x * i + v_y * j + v_z * k
- 또는 v = (v_x, v_y, v_z)
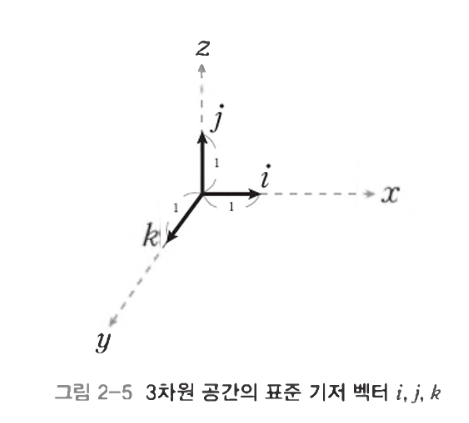
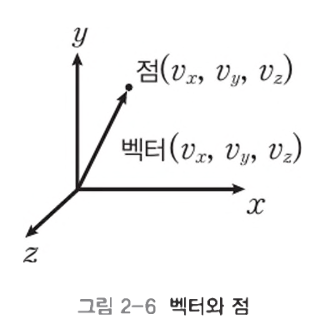
- 위의 경우, 표준 기저 벡터에 곱해지는 스칼라 값들은 각 좌표축 상의 위치값과 같다
- 이는 결국 점을 표현하는 것과 동일하다
- 각 벡터의 덧셈, 뺄셈은 각 x, y, z의 성분을 더해 새로운 값을 만드는 것이다.
- 곱셉은 각 성분에 대해 스칼라를 곱하면 된다
- 뺄셈은 -1의 곱해서 더하는 것이다
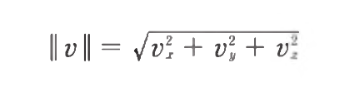
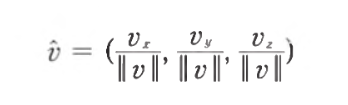
- 벡터의 크기는 피타고라스 정리로 구할 수 있다
- 벡터의 크기가 1이면 이를 단위 벡터 normal vector라고 한다
- 단위 벡터로 만드는 과정을 정규화 normalize라고 한다
벡터 내적 Dot Product
- 두 벡터가 얼마나 같은 방향을 향하고 있는지를 나타낸다
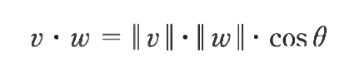
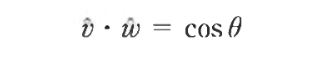
- 두 개의 벡터 값을 이용해서 하나의 스칼라 값을 구하는 연산
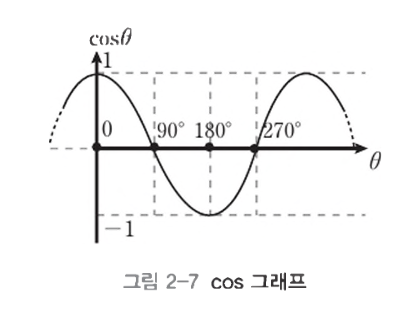
- 두 벡터가 모두 단위 벡터라면, 내적의 값은 두 벡터 사이각의 cos 값이다
- 두 벡터의 길이가 모두 1이기 때문
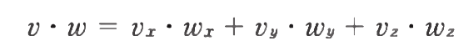
- 위는 또 다른 내적을 구하는 방법
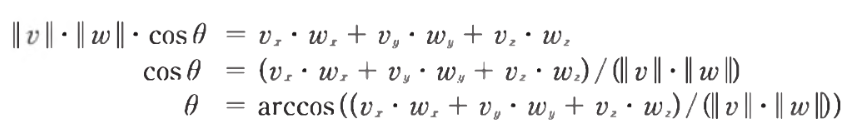
- 위는 실제 사이각을 구하는 방법
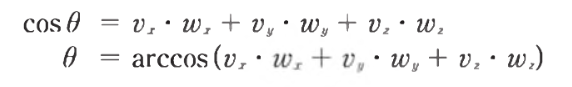
- 위는 두 벡터가 모두 단위벡터인 경우 식을 단편화
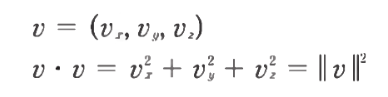
- 위는 자기 자신과 내적을 했을 때의 결과값
- 벡터의 길이의 제곱이 나온다
내적의 사용 예시
- 두 벡터가 모두 영 벡터가 아닐 때 내적 값이 0이면 사이각은 90°이다
- 두 벡터가 모두 영 벡터가 아닐 때 내적 값이 0보다 크면 예각이다
- 0° < A·B
- 두 벡터가 모두 영 벡터가 아닐 때 내적 값이 0보다 작으면 둔각이다
- 0° > A·B

- 0° > A·B
- 두 벡터가 모두 단위 벡터일 때, 내적 값이 -1이면 서로 반대 방향이다
- 두 벡터가 모두 단위 벡터일 때, 내적 값이 1이면 서로 같은 방향이다
- 위의 경우는 두 벡터가 모두 단위 벡터가 아니면 정규화를 해야하는 부담이 있다
- 이런 경우 평행 체크를 할때는, 외적을 사용하는 것이 더 낫다

- 어떤 객체가 기준 점의 앞에 있는지 뒤에 있는지 확인할 수 있다
- cos 값 > 0 이면 앞
- cos 값 < 0 이면 뒤

- 어떤 객체가 특정 시야각 안에 있는지 확인할 수 있다
- 시야각이 cos 값이라고 하고 (Forward 벡터 기준으로 좌우 합이기 때문에 밑에서 /2)
- Forward 벡터와 객체방향의 벡터 A가 있다고 할 때
- F * A < (cos 값/2) 이면 시야 안에 있음
- F * A > (cos 값/2) 이면 시야 밖에 있음
벡터 투영
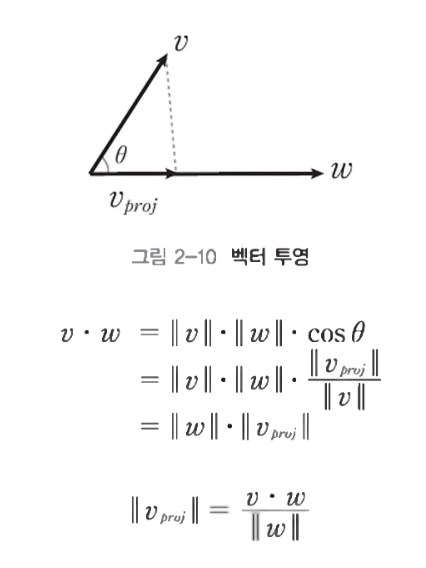
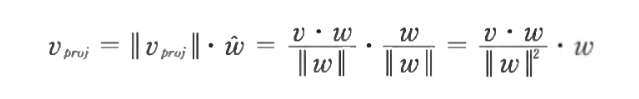
- 벡터 v를 벡터 w에 투영한 벡터 v_proj를 구하기 위해
- 크기를 구하고
- 방향을 스칼라 곱으로 연산한다
- 사실 벡터 w에 적당한 스칼라 값을 곱하는 것과 같다
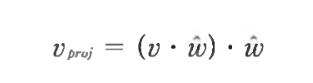
-
위는 w가 단위 벡터인 경우의 연산
- 벡터를 새로운 좌표계, 새로운 표준 기저 벡터들로 표현할 때 사용한다
- 또는 충돌 검사에서도 투영하는 경우가 있다
백터 외적 Cross Product
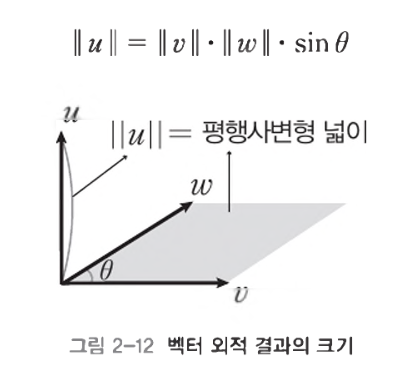
- 연산 결과로 나오는 벡터는 원래 두 벡터에 수직인 새로운 방향이다
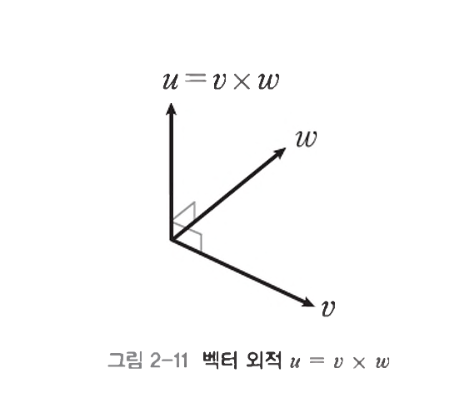
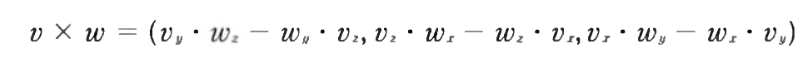
- 두 벡터를 가지고 다른 벡터를 만드는 연산
- 결과 벡터는 두 벡터와 모두 수직이 된다
- 외적은 교환 법칙이 적용되지 않는다
- 결과 벡터의 방향이 반대로 바뀐다
- 외적 결과 벡터의 방향은 오른손 법칙으로 설명할 수 있다
외적의 사용 예시
- 3차원에서 평면을 표현할 때 평면상의 한 점과 평면과 수직인 법선 벡터를 사용
- 두 벡터의 평행 여부를 판단할 때
- 두 벡터가 평행이면 사이각이 0°이거나 180°이면 sin 값이 0
- 두 벡터가 평행이면 평행하변형의 넓이(외적 결과 값)가 0
- 카메라의 Forward, Up 벡터로 카메라 좌표계를 구할 수 있다
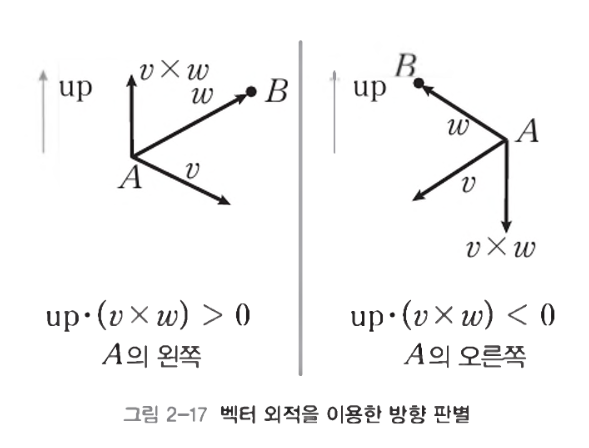
- 객체가 기준 지점의 왼쪽에 있는지 오른쪽에 있는지 확인할 수 있다
- up * (v x w) > 0
- 중점 A를 기준으로 물체 B가 좌측
- 외적 값과 up 벡터의 방향이 동일하게 위쪽
- up * (v x w) < 0
- 중점 A를 기준으로 물체 B가 우측
- 외적 값과 up 벡터의 방향이 서로 반대 (외적 벡터가 아래쪽)
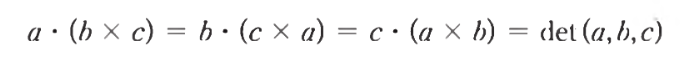
- 좌우 체크의 예시는 위의 스칼라 3중곱을 이용한 것이다
- 벡터 a, b, c로 구성된 행렬의 행렬식 determinant를 의미한다
- 이는 벡터의 평행육면체의 부피를 의미한다
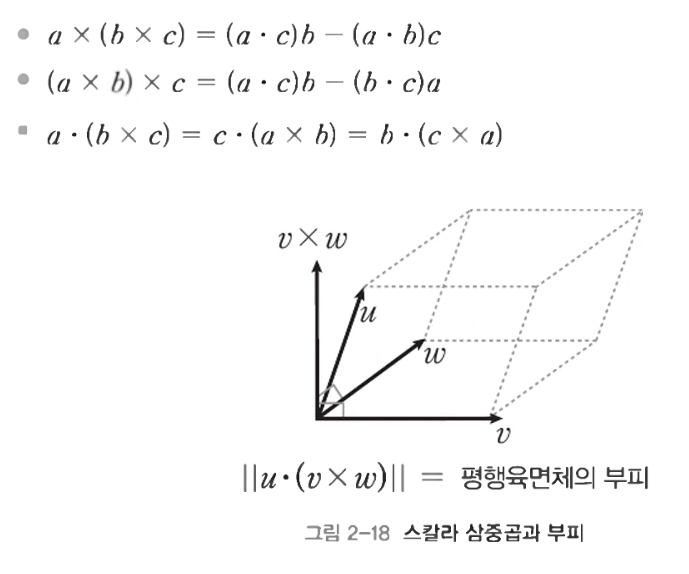
- 아래는 그외 다른 수식들
.jfif)