무방향 그래프 Undirected Graph
방향 그래프 Driected Graph
가중 방향 그래프 Weighted Graph
- 방향 그래프의 간선에 가중치가 부여된 그래프
- Vertex 간 이동하는 데 비용이 발생하고 간선마다 비용이 다름
다익스트라 알고리즘 Dijkstra algorithm
- 1에서 다른 번호까지의 최단 거리를 계산
- 기존의 거리는 비교 후 적은 값으로 업데이트 할 수 있도록 무한대로 초기화
- 인접한 (2), (3), (6)까지의 거리(비용) 비교
- (2) -> 7
- (3) -> 9
- (6) -> 14
- 위 노드 중 가장 거리가 짧은 2번 선택
- 2번에서 주변 노드까지의 거리 계산
- (3) -> 9 (7 + 10 = 17보다 적은 값 유지)
- (4) -> 22 (7 + 15)
- 위 노드 중 가장 거리가 짧은 3번 선택
- 3번에서 주변 노드까지의 거리 계산
- (4) -> 20 (9 + 11 = 20, 22보다 적은 값이므로 갱신)
- (6) -> 11 (9 + 2 = 11, 14보다 적은 값이므로 갱신)
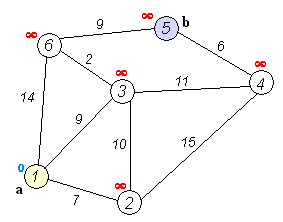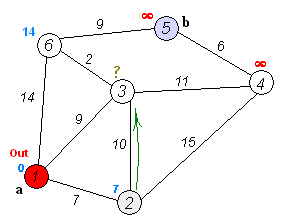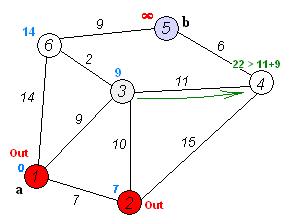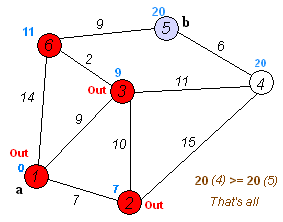
- 위 노드 중 가장 거리가 짧은 6번 선택
- 6번에서 주변 노드까지의 거리 계산
- (5) -> 20 (11 + 9 = 20)
- 최종 1번에서 각 노드까지의 최단거리
- (2) -> 7
- (3) -> 9
- (4) -> 20
- (5) -> 20
- (6) -> 11
- 가중 방향 그래프에서 모든 간선의 가중치가 음이 아닌 경우, 단일 출발점을 가지는 최단 경로 문제를 푸는 방법
- 원래는 두 꼭지점간의 가장 짧은 경로를 찾는 알고리즘
- 두 꼭지점 중 하나를 출발점으로 고정하고, 다른 모든 꼭지점까지의 최단 경로를 찾는 데 사용
function Dijkstra(Graph, source):
create vertex set Q // 미방문 집합 Q
for each vertex v in Graph: // 초기화
dist[v] ← INFINITY // 현재 노드에서 v까지의 아직 모르는 길이
prev[v] ← UNDEFINED // 현재 노드에서 최적 경로의 이전 꼭짓점
add v to Q // 모든 노드는 초기에 Q에 속해있다
dist[source] ← 0 // 현재 노드에서 현재 노드까지의 길이 = 0
while Q is not empty:
u ← vertex in Q with min dist[u] // 집합 Q에서 최소 거리를 갖는 꼭짓점(u)을 가장 먼저 선택
remove u from Q // 그리고 집합에서 제거
for each neighbor v of u: // u의 neighbor을 탐색
alt ← dist[u] + length(u, v) // 현재까지의 거리와 v까지의 거리를 합
if alt < dist[v]: // v 까지의 더 짧은 경로를 찾았을 때 다음 진출할 노드로 선택
dist[v] ← alt
prev[v] ← u
add v to Q
return dist[], prev[]
- 방문하지 않은 꼭지점 중 가장 낮은 값을 가진 곳을 선택
- 방문하지 않은 각 인접 노드와의 거리를 계산
- 작을 경우 인접 거리를 업데이트
A* 알고리즘 A* algorithm
완결성 Completeness
- 경로가 존재하면, 이 경로는 반드시 탐색된다
- Breadth-First, Depth-First, Dijkstra, A* 등이 해당
허용 가능 발견법적 함수 Admissible heuristic = Optimal path
- 최적의 경로 탐색을 보장한다
- 현재 노드에서 목표까지의 추정 비용 ≤ 현재 노드에서 다음 노드까지의 비용 + 다음 노드에서 목표까지의 추정 비용
- 목표에 도달하는 비용을 절대 과대추정하지 않음
- 문제를 푸는 비용이 실제 비용보다 더 작다고 생각한다는 점에서 낙관적
- Greedy Best-First, A* 등이 해당
// 우선순위 큐에 시작 노드를 삽입한다.
// 이 큐는 비용 f(n)이 적을수록 우선 정렬하게 되어있다.
// pq는 openlist
openlist.enqueue(start_node, g(start_node) + h(start_node))
while openlist is not empty // 우선순위 큐가 비어있지 않은 동안
node = openlist.pop // 우선순위 큐에서 pop한다.
if node == goal_node // 만약 해당 노드가 목표 노드이면 반복문 종료
break
// 해당 노드에서 이동할 수 있는 다음 노드들을 보는 동안
for next_node in neighbors
// 우선순위 큐에 다음 노드를 삽입한다.
// 출발점에서 현재 노드까지의 거리 = g(node)
// + 다음 노드로 이동하는 비용 = cost
// + 다음 노드에서 목표지점까지의 heuristic cost = h(goal_node)
// 다음 노드가 open / closed 리스트에 없는 경우, open에 추가
if next_node not on either open or closed list
openlist.push(next_node, g(node) + cost + h(next_node, goal_node))
// 다음 노드가 이미 openlist나 closedlist에 있고, 더 적은 비용이 든다면
// 기존의 old_next_node를 각 리스트에서 삭제하고 업데이트
else if next_node on either open or closed list && cheaper cost
openlist.pop(old_next_node) || closedlist.pop(old_next_node)
openlist.push(next_node, g(node) + cost + h(next_node, goal_node))
// 현재 노드는 방문처리 되어 closed 리스트에 추가
closedlist.push(node)
// 시작 노드에서 목표 노드까지의 거리를 출력한다.
return goal_node_dist
- Openlist - 방문한 상태이고, 다음 노드로 진출 가치가 있는 노드 상태
- Closedlist - 이미 방문한 노드 상태
- None - 아직 방문한 적 없는 노드 상태
출처
